WRITING TWO STEP INEQUALITIES

We can write two-step inequalities to represent real-world problems by translating the words of the problems into numbers, variables, and operations.

Example 1 : 

A mountain climbing team is camped at an altitude of 18,460 feet on Mount Everest. The team wants to reach the 29,029-foot summit within 6 days. Write an inequality to find the average number of feet per day the team must climb to accomplish its objective.

Solution : 

Step 1 :

Identify what you are trying to find. This will be the variable in the inequality.

Let d represent the average altitude the team must gain each day.

Step 2 :

Identify important information in the problem that you can use to write an inequality.

starting altitude : 18,460 ft

target altitude: 29,029 ft

Number of days times altitude gained to reach target altitude : 6 · d

Step 3 : 

Use words in the problem to tie the information together and write an inequality.

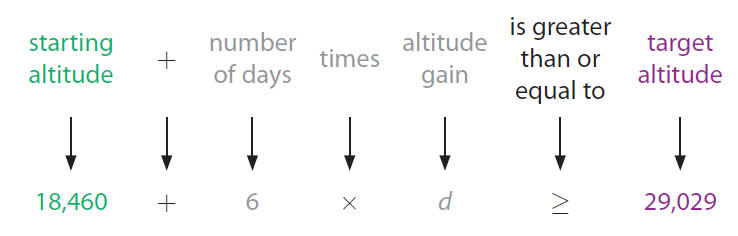
Step 4 : 

Hence, the inequality which represents the given situation is 

18,460 + 6d  ≥  29,029

Example 2 : 

The 45 members of the glee club are trying to raise $6,000 so they can compete in the state championship. They already have $1,240. What inequality can you write to find the amount each member must raise, on average, to meet the goal?

Solution : 

Step 1 :

Identify what you are trying to find. This will be the variable in the inequality.

Let x represent the amount that each member must raise on average to meet the goal. 

Step 2 :

Identify important information in the problem that you can use to write an inequality.

starting balance : $1240

target balance : $6000

Number  of members times amount raised by each member to reach the target balance :  45 · x

Step 3 : 

Use words in the problem to tie the information together and write an inequality.

starting balance ($1240)

+

number of members (45)

times 

amount raised by each member (x)

 ≥

target balance ($6000)

Step 4 : 

Hence, the inequality which represents the given situation is

1240 + 45x  ≥  6000

Example 3 : 

Ella has $40 to spend at the State Fair. Admission is $6 and each ride costs $3. Write an inequality to find the greatest number of rides she can go on.

Solution : 

Step 1 :

Identify what you are trying to find. This will be the variable in the inequality.

Let x represent the total number of rides she can go on.  

Step 2 :

Identify important information in the problem that you can use to write an inequality.

admission : $6

cost of each ride : $3

maximum money can be spent : $40

Number  of rides times cost per ride to reach the maximum money which can be spent :  3 · x

Step 3 : 

Use words in the problem to tie the information together and write an inequality.

admission ($6)

+

aost of each ride ($3)

times 

no. of rides (x)

≤

maximum money can be spent ($40)

Step 4 : 

Hence, the inequality which represents the given situation is

6 + 3x ≤ 40

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.