WRITING THE GIVEN SCALES AS RATIOS AND FIND SCALE FACTOR

When designing a house it would be a ridiculous for an architect to draw a full plan.

Instead the architect draws a smaller diagram in which all measurement have been divided by the same factor and that is called scale factor.

In scale diagrams:

(i)  All lengths have been changed by the same scale factor.

(ii)  All angles are unaltered

Example 1 :

On a scale diagram 1 cm represents 20 m.

a) Write the scale as a ratio.

b) What is the scale factor?

Solution :

1 m  =  100 cm

20 m  =  20 x 100  ==>  2000 cm

(a)  1 : 2000

(b)  So, the scale factor is 2000.

Example 2 :

1 cm represents 10 m

Solution :

1 m  =  100 cm

1 cm : 10 m  ==>  1 cm : 100 cm

So, the scale factor is 100.

Example 3 :

1 cm represents 50 km

Solution :

100 cm  =  1 m

1000 m   =  1 km

1 km  =  100000 cm

50 km  =  5000000 cm

1 cm : 50 km  =  1 : 5000000

So, the scale factor is 5000000.

Example 4 :

1 mm represents 2 m

Solution :

10 mm  =  1 cm

100 cm  =  1 m

2 m  =  1000 mm

1 mm : 2 m  =  1 : 1000

So, the scale factor is 1000.

Example 5 :

1 cm represents 250 km

Solution :

100 cm  =  1 m

1000 m   =  1 km

1 km  =  100000 cm

250 km  =  25000000 cm

1 cm : 250 km  =  1 : 25000000

So, the scale factor is 25000000.

Example 6 :

1 mm represents 5 m

Solution :

10 mm  =  1 cm

100 cm  =  1 m

1 m  =  1000 mm

5 m  =  5000 mm

1 mm : 5 m  =  1 mm : 5000 mm

So, the scale factor is 5000.

Example 7 :

1 cm represents 200 km.

Solution :

100 cm  =  1 m

1000 m  =  1 km

1 km  =  100000 cm

200 km  =  20000000

1 cm : 200 km  =  1 : 20000000

So, the scale factor is 20000000.

Example 8 :

This is a scale diagram of a ship. Use your ruler and the given scale to determine: 

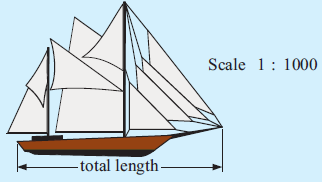
a) the total length of the ship

b) the height of the taller mast

c) the distance between the masts.

Solution :

a) The measured length of the ship is 3.8 cm.

So, the actual length is

= 3:8 cm x 1000

= 3800 cm

= 38 m.

b) The measured height of the taller mast is 2.5 cm

So, the actual height is

= 2:5 cm x 1000

= 2500 cm

= 25 m.

c) The measured distance between the masts = 1.4 cm.

So, the actual distance is

= 1.4 cm x 1000

= 1400 cm

= 14 m.

Example 9 :

A map's scale is 1 inch : 30 miles. The distance between two cities is 45 miles. What is the distance between the cities in map ?

Solution :

1 inch : 30 miles

Let x be the distance between two cities in map.

actual distance between cities = 45 miles.

scale factor = 1/30

1 : 30 = x : 45

1/30 = x/45

1(45) = x(30)

x = 45/30

x = 1.5

So, the distance between two cities is 1.5 inch.

Example 10 :

Most conventional TV screens have a width : height ratio of 4 : 3. If a screen has a width of 42 inches, what is the height ?

Solution :

Scale factor between width to height is = 4 : 3

Width = 42 inches

Let x be the height of the screen.

4 : 3 = 42 : x

4/3 = 42/x

4x = 42(3)

x = 42(3)/4

x = 31.5 inches

So, height of the screen is 31.5 inches.

Example 11 :

Mr. Lloyd wants to build a doll house for his daughter that is proportional to their house. He measured the living room of his house and it is 12 ft by 16 feet. What will be the dimensions of the doll house living room if every foot of the actual house is equal to 1/2 inch in the doll house?

Solution :

Length of actual living room = 12 ft

Width of living room = 16 ft

Length of doll house = 12 x (1/2) = 6 ft

Width of doll house = 16 x (1/2) = 8 ft

So, the measure of doll house is 6 ft by 8 ft.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.