WRITING INEQUALITIES

Writing Inequalities :

An inequality is a statement that two quantities are not equal.

The symbols < and > are used to write inequalities.

•  The symbol > means “is greater than.”
•  The symbol < means “is less than.”

You can use a number line to help write an inequality.

That is,  if we want to write an inequality with two numbers, first we have to locate the numbers on the number line and mark them. 

The number which comes to the right of the other number is greater. The number which comes to the left of the other number is smaller. 

Writing Inequalities - Examples

Example 1 :

Compare the integers -4 and 4

Solution : 

Let us locate the two integers -4 and 4 on a number line and mark them. 

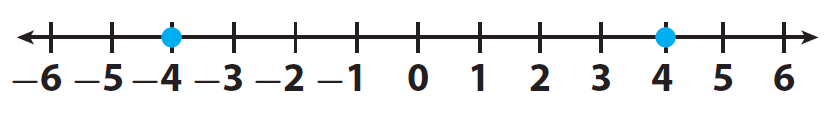
Here, the positive integer 4 comes to the right of -4.

Therefore "4" is greater than "-4"

It can be written as  4 > -4.

And -4 comes to the left of 4.  

Therefore "-4" is smaller than "4"

It can be written as -4 < 4

Example 2 :

Compare the integers -1 and 1

Solution : 

Let us locate the two integers -1 and 1 on a number line and mark them. 

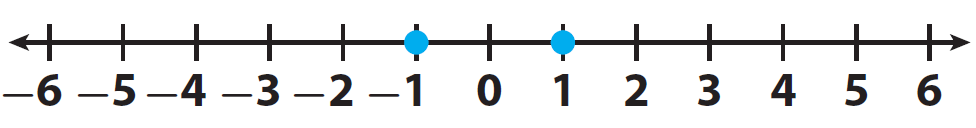
Here, the positive integer 1 comes to the right of -1.

Therefore "1" is greater than "-1"

It can be written as  1 > -1.

And -1 comes to the left of 1.  

Therefore "-1" is smaller than "1"

It can be written as  -1 > 1.

Example 3 :

In 2010, Sacramento, California, received 23 inches in annual precipitation. In 2011, the city received 17 inches in annual precipitation. In which year was there more precipitation ?

Solution : 

Locate the two integers 23 and 17 on a number line and mark them.

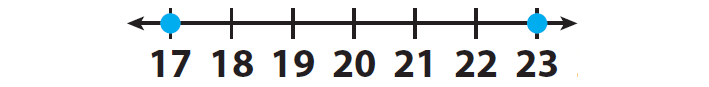
23 is to the right of 17 on the number line.

This means that 23 is greater than 17.

We can write the above situation in terms of inequality as 23 > 17.

17 is to the left of 23 on the number line.

This means that 17 is less than 23.

We can write the above situation in terms of inequality as 17 < 23.

There was more precipitation in 2010.

Example 4 :

An employer recruits experienced (x) and fresh workmen (y) for his firm under the condition that he cannot employ more then 9 people. Find the inequality which can relate "x" and "y". 

Solution :

Given : "x" and "y" stand for number of experienced person and fresh workmen respectively. 

Total number of people recruited  =  x + y 

As per the question, total number of people (experienced + fresh) recruited should not be more than 9. 

That is, total number of people (x+y) recruited should be equal to 9 or less than 9. 

So, we have x + y ≤ 9 

Example 5 :

On the average experienced person does 5 units of work while a fresh one (y) does 3 units of work daily. But the employer has to maintain an output of at least 30 units of work per day. This situation can be expressed as 

Solution :

Given : "x" and "y" stand for number of experienced person and fresh workmen respectively. 

Total number of units of work done by experienced person per day is  5x 

Total number of units of work done by fresh one per day is 3y 

Total number of units of work done by both experienced person and fresh one per day = 5x + 3y 

As per the question, total number of units of work per day should be at least 30 units. 

That is, total number of units of work (5x+3y) should be equal to 30 or more than 30. 

So, we have 5x + 3y ≥ 30 

Example 6 :

The rules and regulations demand that the employer should employ not more than 5 experienced hands (x) to 1 fresh one (y). How can this fact be expressed ? 

Solution :

Given : "x" and "y" stand for number of experienced person and fresh workmen respectively. 

As per the question, no. of experienced hands(x) should not be more than 5 

That is, no. of experienced hands should be equal to 5 or less than 5 

So, we have x ≤ 5 or x/5 ≤ 1 ------(1) 

As per the question, no. of fresh hands is equal to 1 

So, we have y = 1 

In (1), replacing 1 by "y", we get x/5 ≤ y ------(2) 

In (2), multiplying by 5, we get

x ≤ 5y (or) 5y ≥ x 

Example 7 :

The union however forbids the employer to employ less than 2 experienced persons (x) to each fresh person (y). How can this situation be expressed ? 

Solution :

Given : "x" and "y" stand for number of experienced person and fresh workmen respectively. 

In this problem, the word "forbid" plays an important role. 

Meaning of "Forbid" is "Not allowed" 

The union forbids the employer to employ less than 2 experienced hands.

That is, the union does not allow the employer to employ less than 2 experienced hands. 

Therefore, the employer should employ 2 or more than 2 experienced hands. 

So, we have x ≥ 2 or x/2 ≥ 1 ------(1) 

And also, no. of fresh persons to be employed is equal to 1 

So, we have y = 1 

In (1), replacing 1 by "y", we get

x/2 ≥ y or y ≤ x/2 

After having gone through the stuff given above, we hope that the students would have understood, how to write inequalities from the given real world context. 

Apart from the stuff in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.