WRITING INEQUALITIES FROM GRAPHS WORKSHEET

Problem 1 :

Write the inequality for the graph given below.

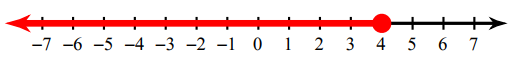
Problem 2 :

Write the inequality for the graph given below.

Problem 3 :

Write the inequality for the graph given below.

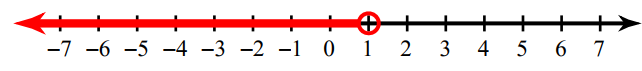
Problem 4 :

Write the inequality for the graph given below.

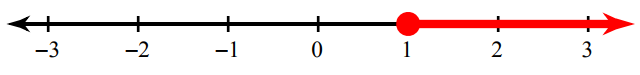
Problem 5 :

Write the inequality for the graph given below.

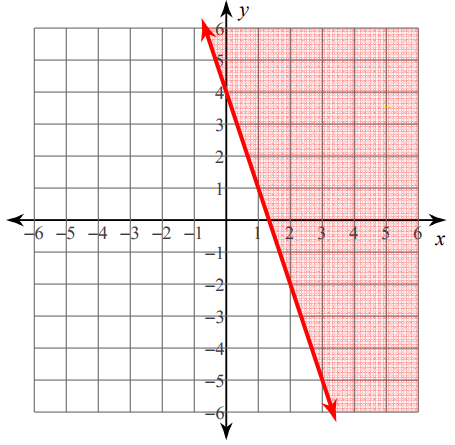
Write the inequality for the graph given below.

Problem 6 :

Problem 7 :

Problem 8 :

Problem 9 :

Problem 10 :

Detailed Answer Key

1. Answer :

In the above graph, we find the filled circle. So we have to use the sign ≤ or ≥.

Now we have to look into the shaded portion. Since the shaded region is in left hand side from the filled circle, we have to use the sign "≤ ".

The inequality for the above graph is x ≤ 4.

2. Answer :

In the above graph, we find the unfilled circle. So we have to use the sign < or >.

Now we have to look into the shaded portion. Since the shaded region is in right hand side from the unfilled circle, we have to use the sign "> ".

The inequality for the above graph is x > -6. 

3. Answer :

In the above graph, we find the unfilled circle. So we have to use the sign < or >.

Now we have to look into the shaded portion. Since the shaded region is in left hand side from the unfilled circle, we have to use the sign "<".

The inequality for the above graph is x  < 1.

4. Answer :

In the above graph, we find the unfilled circle. So we have to use the sign ≤ or ≥.

Now we have to look into the shaded portion. Since the shaded region is in right hand side from the unfilled circle, we have to use the sign "≥".

The inequality for the above graph is x ≥ 1.

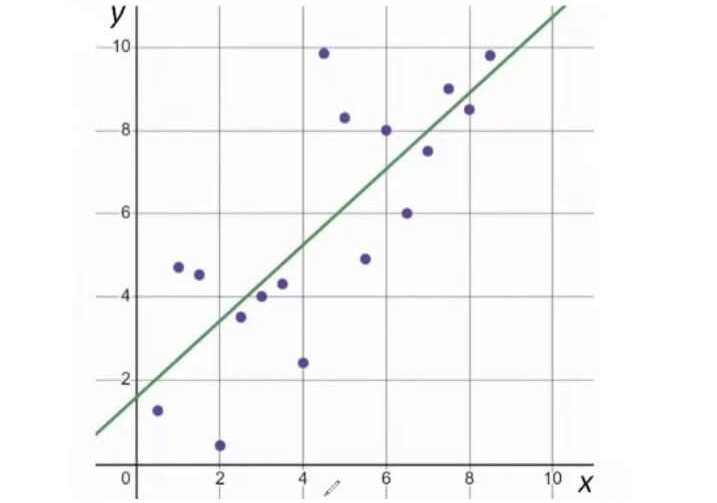
5. Answer :

From the above graph, first let us find the slope and y-intercept.

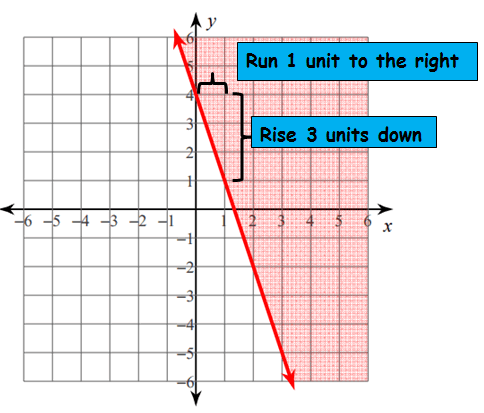
Rise  =  -3 and Run  =  1

Slope  =  -3 / 1  =  -3

y-intercept  =  4

So, the equation of the given line is

y  =  -3x + 4

But we need to use inequality which satisfies the shaded region.

Since the graph contains solid line, we have to use one of the signs ≤  or ≥.

To fix the correct sign, let us take a point from the shaded region.

Take the point (2, 1) and apply it in the equation

y  =  -3x + 4

1  =  -3(2) + 4

1  =  -6 + 4

1  =  - 2

Here 1 is greater than -2, so we have to choose the sign ≥ instead of equal sign in the equation y = -3x + 4.

Hence, the required inequality is

y ≥ -3x + 4

6. Answer :

By observing the shaded region, they are greater than 0.  Since we have transparent circle at 0.

So, the required inequality is x > 0.

7. Answer :

By observing the shaded region, they are greater than 0-5 and lesser than 5.

(or)

The shaded region is in between -5 and 5. Near -5 and 5, we have transparent circle.

So, the required inequality is -5 < x < 5.

8. Answer :

Considering the shaded region, it is below the line. Since it is solid line, we may have to use ≤ or ≥.

y-intercept is 1. Choosing two points on the line, we get (1, 2) and (2, 3).

Slope = (y₂ - y₁) / (x₂ - x₁)

= (3 - 2) / (2 - 1)

= 1/1

= 1

Creating the equation :

y = mx + b

y = 1x + 1

Choosing one of the points from the shaded region is (2, 1).

1 = -1(2) + 1

1 = -2 + 1

1 = -1

To make the statement true, we have to use the inequality sign ≤.

So, the required inequality representing the shaded region in the given figure is y ≤ x + 1

9. Answer :

Considering the shaded region, it is above the line. Since it is dotted line, we may have to use < or >.

y-intercept is 0. Choosing two points on the line, we get (1, 2) and (2, 4).

Slope = (y₂ - y₁) / (x₂ - x₁)

= (4 - 2) / (2 - 1)

= 2/1

= 2

Creating the equation :

y = mx + b

y = 2x + 0

Choosing one of the points from the shaded region is (1, 3).

3 = 2(1) + 0

3 = 2

To make the statement true, we have to use the inequality sign >

So, the required inequality representing the shaded region in the given figure is y > 2x

10. Answer :

The given line is a solid line, we may have to use ≤ or ≥.

y-intercept is 5. Choosing two points on the line, we get (1, 4) and (2, 3).

Slope = (y₂ - y₁) / (x₂ - x₁)

= (3 - 4) / (2 - 1)

= -1/1

= -1

Creating the equation :

y = mx + b

y = -1x + 5

Choosing one of the points from the shaded region is (1, 3).

3 = -1(1) + 5

3 = -1 + 5

3 = 4

To make the statement true, we have to use the inequality sign ≥.

So, the required inequality representing the shaded region in the given figure is y ≥ -1x + 5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.