WRITING EQUIVALENT POLAR COORDINATES

Example 1 :

Sketch (5, 3π/4) and identify 3 other polar coordinates on the interval (-2π, 2π) that represent the same point.

Solution :

First let us plot the point (5, 3π/4) in the polar grid.

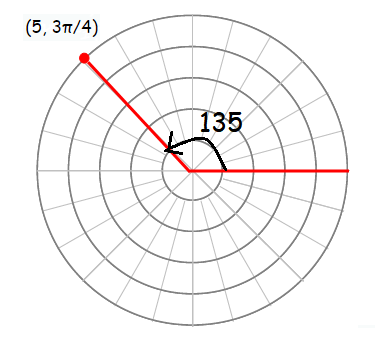
From this position, we can move either clock wise or anti clock wise.

r > 0, θ  =  360 - 135  ==>  225  ==> 5π/4

The another point is (5, 5π/4).

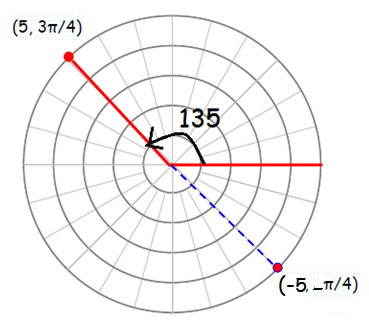
Rotating the ray anticlock wise 135 is equal to rotating the same ray 

If r < 0, then θ  =  π + 3π/4 ==>  7π/4

The point on the terminal side is (-5, 7π/4). So the three remaining points which are equivalent to the given points are  (5, 5π/4), (-5, 7π/4) and 

Example 2 :

Find all polar coordinates of the point (4, 4√3) that describes this point given that 0 <  θ < 2π

Solution :

x  =  4 and y  =  4√3

r cosθ  =  4 and r sin θ  =  4√3

x² + y²  =  r²

4² + (4√3)²  =  r²

r²  =  16 + 16(3)

r²  =  64

r  =  ± 8

If r  =  8 > 0, then θ  =  cos^-1(4/8)

θ  =  cos^-1(1/2)

θ  =  π/3

(8, π/3) and (8, 5π/3).

If r  =  -8 < 0, then θ  =  cos^-1(-4/8)

θ  =  cos^-1(-1/2)

So,

θ  =  2π/3

(-8, 2π/3) and (8, 4π/3).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.