AREA OF TRAPEZOID WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
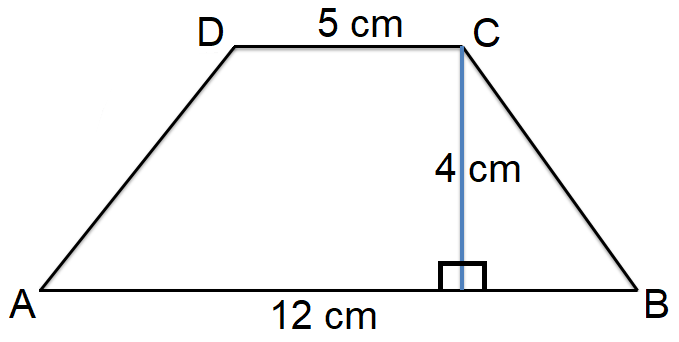
Find the area of the trapezoid ABCD shown below.
Problem 2 :
In a trapezoid the measurement of one parallel side two more than the other parallel side and the height is 4 cm. The area of the trapezoid is 64 cm2. Find the lengths of the two parallel sides.
Problem 3 :
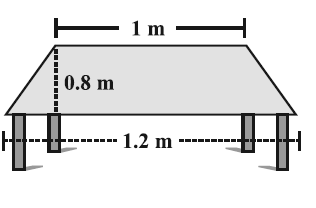
The shape of the top surface of a table is a trapezoid. Find its area, if its parallel sides are 1 m and 1.2 m and perpendicular distance between 0.8 m.
Problem 4 :
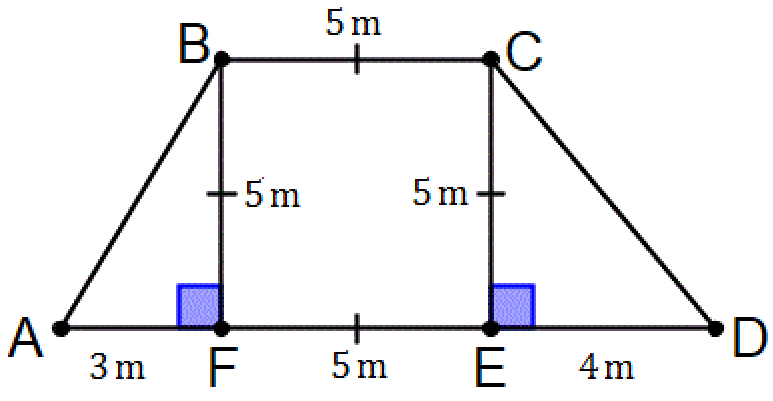
The wall is in the shape as shown below has to be painted. If one can of paint covers 0.5 m2, how many cans of paint will be needed, if only one coat of paint is applied ?

Problem 1 :
Find the area of the trapezoid ABCD shown below.

Solution :
Area of the trapezoid ABCD is
= (1/2)(a + b)h
Substitute a = 5, b = 12 and h = 4.
= (1/2)(5 + 12)4
= (1/2)(17)4
= 34 cm2
Problem 2 :
In a trapezoid the measurement of one parallel side two more than the other parallel side and the height is 4 cm. The area of the trapezoid is 64 cm2. Find the lengths of the two parallel sides.
Solution :
Let 'a' and 'b' be the two parallel sides.
One parallel side is two more than the other parallel side.
Then,
a = b + 2
Area of the trapezium = 64 cm2
(1/2)(a + b)h = 64
Substitute h = 4 and a = b + 2.
(1/2)(b + 2 + a)4 = 64
(2b + 2)2 = 64
Divide each side by 2.
2b + 2 = 32
Subtract 2 from each side.
2b = 30
Divide each side by 2.
b = 15
Then,
a = b + 2
a = 15 + 2
a = 17
So, the lengths of the two parallel sides are 15 cm and 17 cm.
Problem 3 :
The shape of the top surface of a table is a trapezoid. Find its area, if its parallel sides are 1 m and 1.2 m and perpendicular distance between 0.8 m.

Solution :
Area of a the top of surface of the table (trapezoid) is
= (1/2)(a + b)h
= (1/2)(1.2 + 1)0.8
= (1/2) (2.2)0.8
= 1.1 (0.8)
= 8.8 m2
Problem 4 :
The wall is in the shape as shown below has to be painted. If one can of paint covers 0.5 m2, how many cans of paint will be needed, if only one coat of paint is applied ?

Solution :
In the figure shown above, the perpendicular distance between the two sides BC and AB at any point is same, which is 5 cm.
Then, the sides BC and AD are parallel.
In the quadrilateral above, because the two sides BC and AD are parallel, ABCD is a trapezoid.
Let 'a' and 'b' be the lengths of two parallel sides and.
a = BC = 5cm
b = AD = AF + FE + ED = 3 + 5 + 4 = 12 cm
Height (h) = 5 cm
Area of the trapezoid ABCD is
= (1/2)(a + b)h
Substitute a = 5, b = 12 and h = 5.
= (1/2)(5 + 12)5
= 42.5 m2
One can of paint covers 0.5 m2.
Number of cans of paint required 42.5 m2 is
= 42.5 / 0.5
= 425 / 5
= 85
So, 85 cans of paint required to cover the above wall.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Dec 31, 25 09:15 PM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations -
Solving the HARDEST SAT Math Questions ONLY using Desmos
Dec 31, 25 05:53 AM
Solving the HARDEST SAT Math Questions ONLY using Desmos -
Times Table Shortcuts
Dec 30, 25 07:14 PM
Times Table Shortcuts - Concept - Examples
