WRITING EQUATIONS TO REPRESENT SITUATIONS

Example 1 :

Sarah used a gift card to buy $47 worth of food. She has $18 left on her gift card. Write an equation to represent this situation.

Solution :

Write a word equation based on the situation.

Rewrite the equation using a variable for the unknown quantity and the given values for the known quantities.

Let x be the amount on the card.

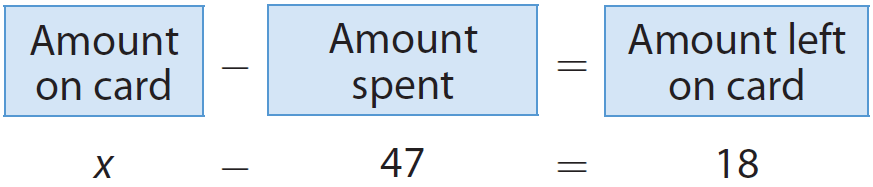
Hence, the equation "x - 47 = 18" represents the given situation.

Example 2 :

The sum of a number f and 9 is equal to 38. Write an equation to represent this situation.

Solution :

In Math, "sum" means, we have to add.

From the information "The sum of a number f and 9", we have

f + 9

Since, the sum of a number f and 9 is equal to 38, we have

f + 9 = 38

Hence, the equation "f + 9 = 38" represents the given situation.

Example 3 :

Kim rented skates for h hours. The rental fee was $2 per hour. She paid a total of $8.  Write an equation to represent this situation.

Solution :

For each hour Kim rented skates, she has to pay $2.

Since she rented skates for "h" hours, total money paid is the product of "h" and $2.

That is,

2h

But it is given that she paid a total of $8.

Then, we have

2h = 8

Hence, the equation "2h = 8" represents the given situation.

Example 4 :

The denominator of a fraction exceeds the numerator by 5. If 3 be added to both, the fraction becomes 3/4. Write an equation to represent this situation.

Solution :

First assign variable for unknown quantity.

Let "x" be the numerator.

The relationship between the numerator and denominator is

"The denominator of a fraction exceeds the numerator by 5"

Then, we have

x/(x + 5)

From the information, "If 3 be added to both, the fraction becomes 3/4", we have

(x + 3)/(x + 5 + 3) = 3/4

(x + 3)/(x + 8) = 3/4

Hence, the equation "(x + 3)/(x + 8) = 3/4" represents the given situation.

Example 5 :

John is paid $8 more than the number of bags of peanuts he sells at the baseball stadium. The table given below shows the relationship between the money John earns and the number of bags of peanuts John sells. Identify the independent and dependent variables, and write an equation to represent  this situation. 

Solution :

The number of bags is the independent variable, and the money John earns is the dependent variable.

Since "x" stands for number of bags and it is given that he earns $8 more than number of bags (x), the money earned by John is

x + 8

Since "y" stands for money earned by John, we have

y = x + 8

Hence, the equation "y = x + 8" represents the given situation.

Example 6 :

A taxi charges a flat rate of $3, plus an additional $1.50 per mile. Write an equation to represent this situation.   

Solution :

Let "x" be the number of miles and "y" be the total fare for "x" number of miles.

Since taxi, charges $1.50 per mile, fare for "x" number of miles is

1.5x

Taxi charges a flat rate of $3. Then the total fare is

1.5x + 3

Since  "y" stands for total fare for "x" number of miles, we have

y = 1.5x + 3

Hence, the equation "y = 1.5x + 3" represents the given situation.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.