WRITING AND EVALUATING EXPRESSIONS

In this section, you will learn how to write a mathematical expression from a verbal description and evaluate expressions for the given values of the variables or unknowns.  

Writing Expression from a Verbal Phrase 

Let us see, how to write a verbal phrase as an expression.

If there is any unknown value in the given verbal phrase, replace it by some English alphabet. 

Example 1  

Example 2

Example 3

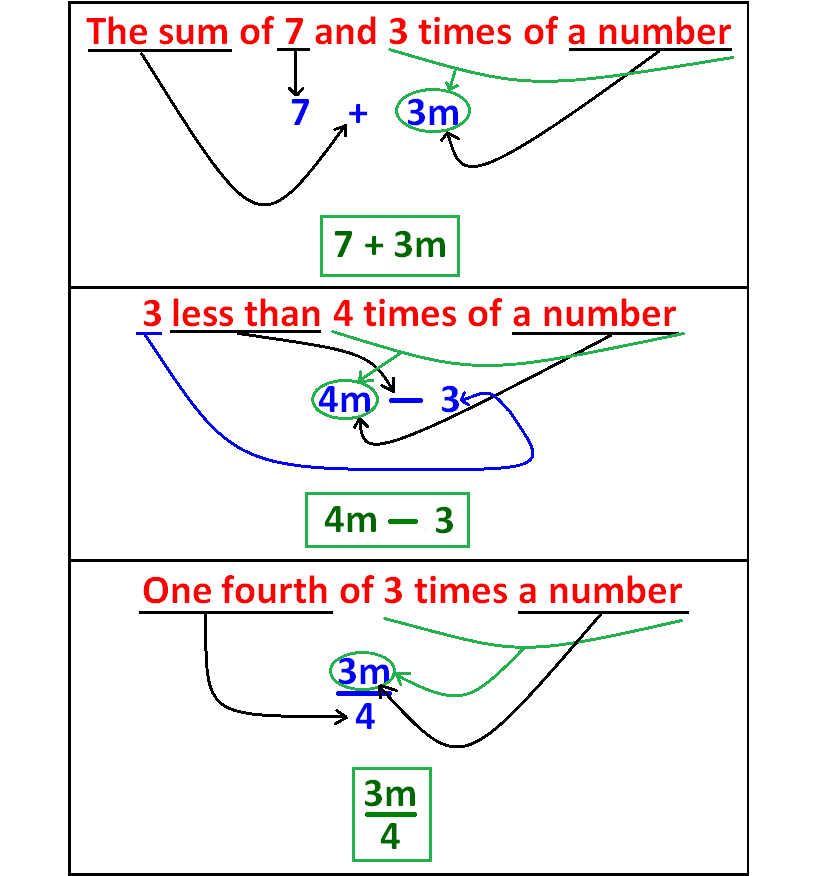
Writing Expressions - Practice Questions

Question 1 :

Write the given verbal phrase into mathematical expression

"The sum of 5 times a number and 8"

Answer :

5x + 8

Question 2 :

Write the given verbal phrase into mathematical expression

"2 times the sum of 7 times a number and 4"

Answer :

2(7x + 4)

Question 3 :

Write the given verbal phrase into mathematical expression

"7 less than 4 times a number"

Answer :

4x - 7

Question 4 :

Write the given verbal phrase into mathematical expression

"One fifth of sum of 3 times a number and 9"

Answer :

(3x + 9) / 5

Question 5 :

Write the given verbal phrase into mathematical expression

"One seventh of 3 less than 4 times a number"

Answer :

(4x - 3) / 7

Question 6 :

Write the given verbal phrase into mathematical expression

"5 times of a number is decreased by 8"

Answer :

5x - 8

Question 7 :

Write the given verbal phrase into mathematical expression

"6 times of a number is increased by 15"

Answer :

6x + 15

Question 8 :

Write the given verbal phrase into mathematical expression

"7 less than 3 times the sum of a number and 6"

Answer :

3(x + 6) - 7

Question 9 :

Write the given verbal phrase into mathematical expression

"3 times the difference between a number and 8"

Answer :

3(x - 8)

Question 10 :

Write the given verbal phrase into mathematical expression

"One fourth of 3 times the difference between a number and 6"

Answer :

3(x - 6) / 4

Evaluating Expressions - Practice Questions

Question 1 :

Evaluate the given expression for x  =  3 and y  =  5. 

3x + 2y

Answer :

Substitute  3 for x and 5 for y into the given expression.

3x + 2y  =  3(3) + 2(5)

3x + 2y  =  9 + 10

3x + 2y  =  19

Question 2 :

Evaluate the given expression for m  =  5 and n  =  2. 

m² + 2mn²

Answer :

Substitute 5 for m and 2 for n into the given expression.

m² + 2mn²  =  5² + 2(5)(2)²

m² + 2mn²  =  25 + 40

m² + 2mn²  =  65

Question 3 :

Evaluate the given expression for s  =  5. 

s² + 7s - 2

Answer :

Substitute 5 for s into the given expression.

s² + 7s - 2  =  5² + 7(5) - 2  

s² + 7s - 2  =  25 + 35 - 2  

s² + 7s - 2  =  58

Question 4 :

Evaluate the given expression for m  =  1/3. 

18m² + 3m + 7

Answer :

Substitute 1/3 for m into the given expression.

18m² + 3m + 7  =  18(1/3)² + 3(1/3) + 7  

18m² + 3m + 7  =  2 + 1 + 7  

18m² + 3m + 7  =  10

Question 5 :

Evaluate the given expression for m  =  13. 

m² + m - 54

Answer :

Substitute 13 for s into the given expression.

m² + m - 54  =  13² + 13 -54  

m² + m - 54  =  169 + 13 - 54  

m² + m - 54  =  128

Question 6 :

Evaluate the given expression for x  =  3  and y  =  5. 

x² + y²

Answer :

Substitute 3 for x and 5 for y into the given expression.

x² + y²  =  3² + 5²

x² + y²  =  9 + 25

x² + y²  =  34

Question 7 :

Evaluate the given expression for m  =  5 and n  =  2. 

5m² + 2m²n

Answer :

Substitute 5 for m and 2 for n into the given expression.

5m² + 2m²n  =  5(5)² + 2(5)²(2)

5m² + 2m²n  =  5(25) + 2(25)(2)

5m² + 2m²n  =  125 + 100

5m² + 2m²n  =  225

Question 8 :

Evaluate the given expression for s  =  6. 

s² - 3s + 10

Answer :

Substitute 6 for s into the given expression.

s² - 3s + 10  =  6² - 3(6) + 10

s² - 3s + 10  =  36 - 18 + 10

s² - 3s + 10  =  28

Question 9 :

Evaluate the given expression for x  =  2  and y  =  -5. 

x² - 3y²

Answer :

Substitute 2 for x and -5 for y into the given expression.

x² - 3y²  =  2(2)² - 3(-5)²

x² - 3y²  =  2(4) - 3(25)

x² - 3y²  =  8 - 75

x² - 3y²  =  -77

Question 10 :

Evaluate the given expression for m  =  3. 

(2m² + 5m - 7) / 2

Answer :

Substitute 3 for m into the given expression.

(2m² + 5m - 7) / 2  =  [2(3)² + 5(3) - 7] / 2

(2m² + 5m - 7) / 2  =  [2(9) + 15 - 7 ] / 2

(2m² + 5m - 7) / 2  =  (18 + 15 - 7) / 2

(2m² + 5m - 7) / 2  =  26 / 2

(2m² + 5m - 7) / 2  =  13

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.