WRITING AN EQUATION FOR A PROPORTIONAL RELATIONSHIP

If there is a proportional relationship between the two variables "x" and "y", we can write the relationship between them using an equation. 

There are two types of proportional relationships. 

1.  Direct proportion

2.  Inverse proportion

Direct Proportion - Concept

If x gets increased, y also gets increased

or

If x gets decreased, y also gets decreased 

Then, x is directly proportional to y. And x and y can be related by the equation given below.

y  =  kx

Inverse Proportion - Concept

If x gets increased, y gets decreased

or

If x gets decreased, y gets increased 

Then, x is inversely proportional to y. And x and y can be related by the equation given below. 

y  =  k/x

The variable k is called the constant of proportionality, and it represents the constant rate of change or constant ratio between x and y.

Example 1 :

Examine the given table and determine if the relationship is proportional. If yes, write the equation which relates hours and miles. 

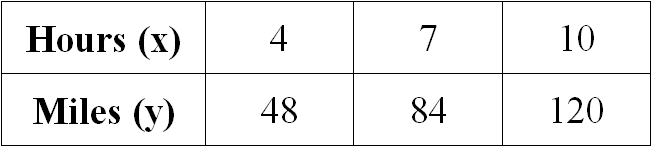
Solution : 

Let us get the ratio of x and y for all the given values. 

4 / 48  =  1 / 12

7 / 84  =  1 / 12

10 / 120  =  1 / 12

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore the relationship given in the table is proportional.   

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion. 

Then, we have 

y  =  kx 

Substitute x = 4 and y = 48.

48  =  k(4)

12  =  k

So, the required equation is y = 12x.

Example 2 :

Examine the given table and determine if the relationship is proportional. If yes, write the equation which relates days and pages read. 

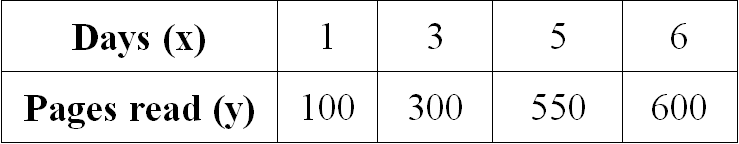
Solution : 

Let us get the ratio of x and y for all the given values. 

1 / 100  =  1 / 100

3 / 300  =  1 / 100

5 / 550  =  1 / 110

6 / 600  =  1 / 100

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

Therefore the relationship given in the table is not proportional.  

Example 3 :

Examine the given table and determine if the relationship is proportional. If yes, write the equation which relates cups of flour and loaves of bread. 

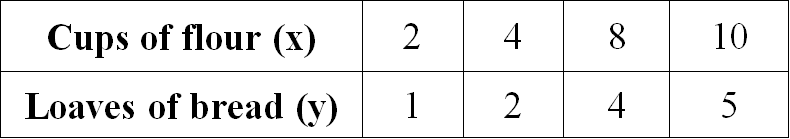
Solution : 

Let us get the ratio of x and y for all the given values. 

2 / 1  =  2

4 / 2  =  2

8 / 4  =  2

10 / 5  =  2

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore the relationship given in the table is proportional.   

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion. 

Then, we have 

y  =  kx 

Substitute x = 2 and y = 1.

1  =  k(2)

1 / 2  =  k

So, the required equation is y = (1/2)x.

Example 4 :

Examine the given table and determine if the relationship is proportional. If yes, write the equation which relates number of socks and cost.

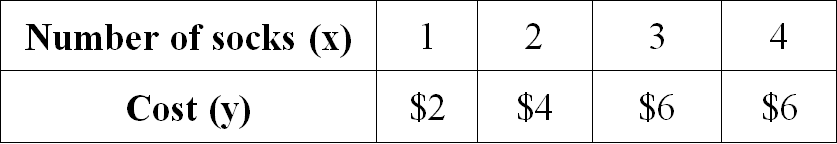
Solution : 

Let us get the ratio of x and y for all the given values. 

1 / 2  =  1 / 2

2 / 4  =  1 / 2

3 / 6  =  1 / 2

4 / 6  =  2 / 3

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

Therefore the relationship given in the table is not proportional.

Example 5 :

Examine the given table and determine if the relationship is proportional. If yes, write the equation which relates hours worked and money earned. 

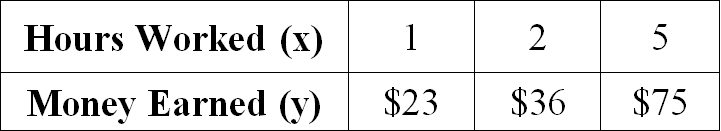
Solution : 

Let us get the ratio of x and y for all the given values. 

1 / 23  =  1 / 23

2 / 36  =  1 / 18

5 / 75  =  1 / 15

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

Therefore the relationship given in the table is not proportional.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

You can also visit the following web pages on different stuff in math. 

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractrions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6