WRITE INEQUALITIES FROM GRAPHS

Inequalities in One Variable from Graphs

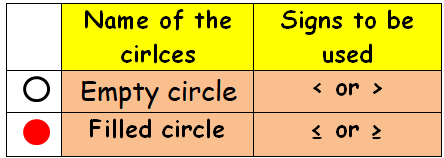
In the graph of an inequality in one variable, if there is empty circle, we have to use < and > in the inequality. 

In the graph of an inequality in one variable, if there is filled circle, we have to use ≤ and ≥ in the inequality. 

More clearly, 

Example 1 :

Write the inequality for the graph given below.

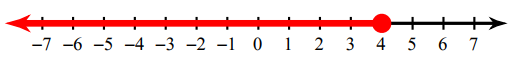
Solution :

In the above graph, we find the filled circle. So we have to use the sign ≤ or ≥.

Now we have to look into the shaded portion. Since the shaded region is in left hand side from the filled circle, we have to use the sign "≤ ".

The inequality for the above graph is x ≤ 4.

Example 2 :

Write the inequality for the graph given below.

Solution :

In the above graph, we find the unfilled circle. So we have to use the sign < or >.

Now we have to look into the shaded portion. Since the shaded region is in right hand side from the unfilled circle, we have to use the sign "> ".

The inequality for the above graph is x > -6. 

Example 3 :

Write the inequality for the graph given below.

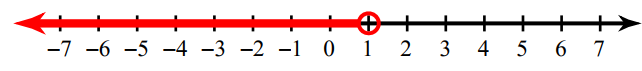
Solution :

In the above graph, we find the unfilled circle. So we have to use the sign < or >.

Now we have to look into the shaded portion. Since the shaded region is in left hand side from the unfilled circle, we have to use the sign "<".

The inequality for the above graph is x  < 1.

Example 4 :

Write the inequality for the graph given below.

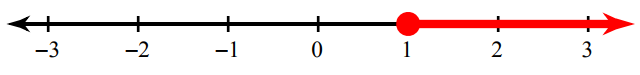
Solution :

In the above graph, we find the unfilled circle. So we have to use the sign ≤ or ≥.

Now we have to look into the shaded portion. Since the shaded region is in right hand side from the unfilled circle, we have to use the sign "≥".

The inequality for the above graph is x ≥ 1.

Inequalities in Two Variables from Graph

To find linear inequalities in two variables from graph, first we have to find two information from the graph. 

(i) Slope 

(ii) y -intercept

By using the above two information we can easily get a linear linear equation in the form y = mx + b.

Here "m" stands for slope and "b" stands for y-intercept.

Now we have to notice whether the given line is solid line or dotted line.

• If the graph contains the dotted line, then we have to use one of the signs < or >.
• If the graph contains the solid line, then we have to use one of the signs ≤  or ≥. 

Example 5 :

Write the inequality for the graph given below.

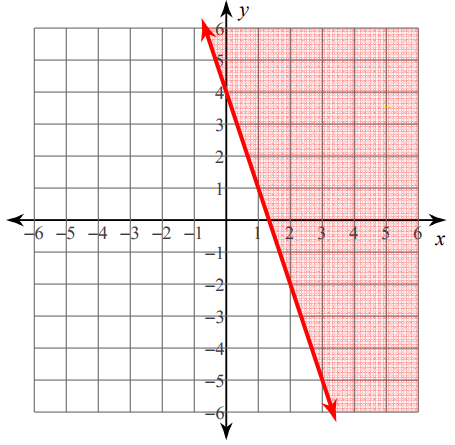
Solution :

From the above graph, first let us find the slope and y-intercept.

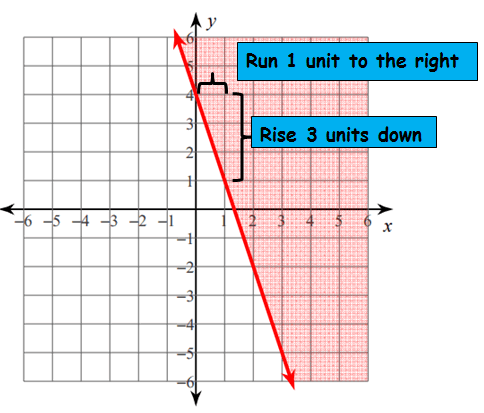
Rise  =  -3 and Run  =  1

Slope  =  -3 / 1  =  -3

y-intercept  =  4

So, the equation of the given line is

y  =  -3x + 4

But we need to use inequality which satisfies the shaded region.

Since the graph contains solid line, we have to use one of the signs ≤  or ≥.

To fix the correct sign, let us take a point from the shaded region.

Take the point (2, 1) and apply it in the equation

y  =  -3x + 4

1  =  -3(2) + 4

1  =  -6 + 4

1  =  - 2

Here 1 is greater than -2, so we have to choose the sign ≥ instead of equal sign in the equation y = -3x + 4.

Hence, the required inequality is

y ≥ -3x + 4

Example 6 :

Which graph shows the solutions of -2(1 - x) < 3(x - 2) ?

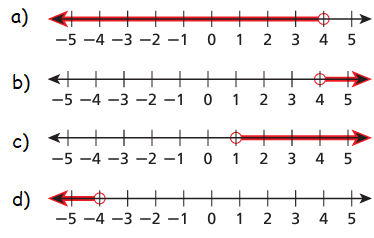
Solution :

-2(1 - x) < 3(x - 2)

Distributing -2 and 3 on both sides, we get

-2 + 2x < 3x - 6

Subtracting 3x on both sides

2x - 3x - 2 < -6

Adding 2 on both sides

-x - 2 < -6

-x < -6 + 2

-x < -4

Multiplying by -1 on both sides. While multiplying by negative, we have to flip the inequality sign.

x > 4

All values greater than 4 will be solution. So, option a is correct.

Example 7 :

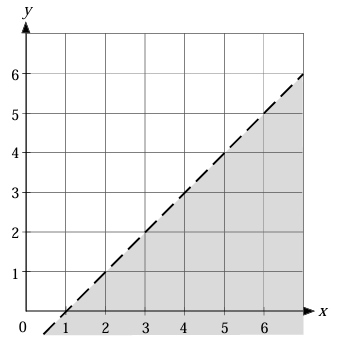
Considering the shaded region, it is below the line. Since it is dotted line, we may have to use < or >.

We don't see the y-intercept in the given figure. Choosing two points on the line, we get (2, 1) and (3, 2).

Slope = (y₂ - y₁) / (x₂ - x₁)

= (2 - 1) / (3 - 2)

= 1/1

= 1

Creating the equation :

y = mx + b

y = 1x + b

Applying the point (3, 2) in the equation above,

2 = 1(3) + b

2 = 3 + b

b = 2 - 3

b = -1

Applying the y-intercept, we get

y = x - 1

Choosing one of the points from the shaded region is (3, 1).

1 = 1(3) - 1

1 = 3 - 1

1 = 2

To make the statement true, we have to use the inequality sign <.

So, the required inequality representing the shaded region in the given figure is y < x - 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.