WRITE LINEAR EQUATIONS IN STANDARD FORM

Standard Form of a Linear Equation

Ax + By  =  C

Example 1 :

Write the following linear equation in standard form.

y  =  3x + 1

Solution :

y  =  3x + 1

Subtract 3x from each side. 

-3x + y  =  1

Multiply each side by -1.

3x - y  =  -1

Example 2 :

Write the following linear equation in standard form.

y  =  x/2 - 3

Solution :

y  =  x/2 - 3

Multiply each side by 2.

2y  =  x - 6

Subtract x from each side. 

-x + 2y  =  -6

Multiply each side -1.

x - 2y  =  6

Example 3 :

Write the following linear equation in standard form.

y  =  1/4 - 7x/2

Solution :

y  =  1/4 - 7x/2

On the right side of the equation, we find the denominators 4 and 2. 

Find the least common multiple of 4 and 2 and multiply both sides of the equation by it to get rid of the denominators. 

Least common multiply of (4, 2) is 4.

Multiply each side of the above equation by 4. 

4y  =  1 - 14x

Add 14x to each side. 

14x + 4y  =  1

Example 4 :

Write the following linear equation in standard form.

y  =  -5x/4 + 1/6

Solution :

y  =  -5x/4 + 1/6

On the right side of the equation, we find the denominators  4 and 6. 

Find the least common multiple of 4 and 6 and multiply both sides of the equation by it to get rid of the denominators. 

Least common multiply of (4, 6) is 12.

Multiply each side of the above equation by 12. 

12y  =  -15x + 2

Add 15x to each side. 

15x + 12y  =  2

Example 5 :

The line y = kx + 4, where k is a constant is graphed in the xy-plane. If the line contains the point (c, d) where c ≠ 0 and d ≠ 0, what is the slope of the line in terms of c and d ?

a)  (d - 4) / c     b)  (c - 4) / d      c) (4 - d) / c

d)  (4 - c) / d

Solution :

y = kx + 4

The line contains the point (c, d).

d = k(c) + 4

d = kc + 4

kc = d - 4

k = (d - 4) / c

So, option a is correct.

Example 6 :

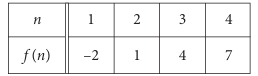
The table above shows some values of the linear function f. Which of the following defines f ?

a)  f(n)  = n - 3    b)  f(n) = 2n - 4   c)  f(n) = 3n - 5

d)  f(n) = 4n - 6

Solution :

The points on the line (1, -2) and (2, 1).

Slope = (y₂ - y₁) / (x₂ - x₁)

= (1 - (-2)) / (2 - 1)

= (1 + 2) / 1

= 3

y = mx + b

Applying slope = 3, we get

y = 3x + b

Applying the point (2, 1), we get

1 = 3(2) + b

1 = 6 + b

b = 1 - 6

b = -5

f(n) = 3x - 5 is the required equation.

Example 7 :

The average number of students per classroom at Central High School from 2000 to 2010 can be modeled by the equation y = 0.56x + 27.2, where x represents the number of years since 2000, and y represents the average number of students per classroom. Which of the following best describes the meaning of the number 0.56 in the equation ?

a)  The total number of students at the school in 2000.

b)  The average number of students per classroom in 2000.

c)  The estimated increase in the average number of students per classroom each year.

d)  The estimated difference between the average number of students per classroom in 2010 and in 2000.

Solution :

y = 0.56x + 27.2

Comparing with y = mx + b

slope (m) = 0.56

The average number of students per classroom in 2000. So, option b is correct.

Example 8 :

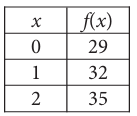
For the linear function f, the table shows three values of x and their corresponding values of f(x), which equation defines f(x) ?

a) f(x) = 3x + 29           b)  f(x) = 29x + 32

c)  f(x) = 35x + 29        d)  f(x) = 32x + 35

Solution :

(0, 29) and (1, 32)

Slope = (32 - 29) / (1 - 0)

= 3

y = mx + b

y = 3x + b

Applying the point (0, 29), we get

29 = 3(0) + b

29 = b

y = 3x + 29

is the required equation.

Example 9 :

Hana deposited a fixed amount into her bank account each month. The function f(t) = 100 + 25t gives the amount in dollars, in Hana's bank account after t monthly deposits. What is the best interpretation of 25 in this context ?

a) With each monthly deposit, the amount in Hana's bank account increased by $25.

b)  Before Hana made any monthly deposits, the amount in her bank account was $25.

c)  After 1 monthly deposit, the amount in Hana's bank account was $25

d)  Hana's made a total of 25 monthly deposits.

Solution :

f(t) = 100 + 25t

With each monthly deposit, the amount in Hana's bank account increased by $25. So, option a is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.