WORKSHEET ON WORD PROBLEMS ON RATIO AND PROPORTION

Problem 1 :

The sum of two numbers is 100. If the ratio between the two numbers is 2 : 3, find the numbers.

Problem 2 :

If the angles of a triangle are in the ratio 2 : 7 : 11, then find the angles.

Problem 3 :

The ratio of two numbers is 7 : 10. Their difference is 105. Find the numbers.

Problem 4 :

A, B and C are three cities. The ratio of average temperature between A and B is 11:12 and that between A and C is 9 : 8. Find the ratio between the average temperature of B and C.

Problem 5 :

The ratio between the speeds of two trains is 7 : 8. If the second train runs 400 miles in 5 hours, then, find the speed of the first train.

Problem 6 :

Find in  what ratio will the total wages of the workers of a factory be increased or decreased, if there be a reduction in the number of workers in the ratio 15:11 and an increment in their wages in the ratio 22 : 25.

Problem 7 :

If $782 is divided among three persons A, B and C in the ratio 1/2 : 2/3 : 3/4, then   find the share of A.

Problem 8 :

An amount of money is to be divided among P, Q and R in the ratio  3 : 7 : 12. The difference between the shares of P and Q is $2400. What will be the difference between the shares of Q and R?

1. Answer :

From the given ratio 2 : 3,

first number = 2x

second number = 3x

Given : The sum of the two numbers is 100.

2x + 3x = 100

5x = 100

Divide both sides by 5

x = 20

Therefore,

first number = 2(20) = 40

second number = 3(20) = 60

2. Answer :

From the ratio 2 : 7 : 11, the three angles can be assumed to be

2x, 7x, 11x

In any triangle, sum of the angles is equal to 180°.

2x + 7x + 11x = 180°

20x = 180

x = 9

Then,

the first angle = 2x = 2 ⋅ 9 = 18°

the second angle = 7x = 7 ⋅ 9 = 63°

the third angle = 11x = 11 ⋅ 9 = 99°

Hence the angles of the triangle are (18°, 63°, 99°).

3. Answer :

From the given ratio 7 : 10, the two number can be assumed to be

7x,  10x

The difference between the numbers is 105.

10x - 7x = 105

3x = 105

x = 35

Then,

the first number = 7x = 7 ⋅ 35 = 245

the second number = 10x = 10 ⋅ 35 = 350

Hence the numbers are 245 and 350.

4. Answer :

From A : B = 11 : 12 and A : C = 9 : 8, we find A in common.

The values corresponding to A  in both the ratios are different.

First we have to make them to be same.

value corresponding to A in the 1^st ratio = 11

value corresponding to A in the 2^nd ratio = 9

L.C.M of (11, 9) = 99.

First ratio ----> A : B = 11 : 12 = (11 ⋅ 9) : (12 ⋅ 9) = 99 : 108

Second ratio ----> A : C = 9 : 8 = (9 ⋅ 11) : (8 ⋅ 11) = 99 : 88

Clearly,

A : B = 99 : 108 ----(1)

A : C = 99 : 88 ----(2)

Now, the values corresponding to A  in both the ratios are same.

From (1) and (2), we get

B : C = 108 : 88

Simplify.

B : C = 27 : 22

Hence, the ratio between the average temperature of B and C is

27 : 22

5. Answer :

From the given ratio 7 : 8, we have

speed of the first train = 7x ----(1)

speed of the second train = 8x ----(2)

Second train runs 400 miles in 5 hours  (given)

[Hint : Speed = Distance/Time]

So, speed of the second train  is

= 400/5

= 80 mph ----(3)

From (2) and (3), we get

8x = 80

x = 10

From (1), speed of the first train is

= 7x

= 7 ⋅ 10

= 70

Hence, the speed of the first train is 70 mph.

6. Answer :

Let x be the number of workers and y be the average wages per worker.

Then, total wages = (no. of workers) x (wages per worker)

Total wages = xy or 1xy ----(1)

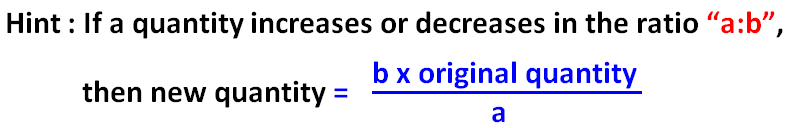
After reduction in workers in the ratio 15 : 11,

no. of workers = 11x/15

After increment  in wages in the ratio 22 : 25,

wages per worker = 25y/22

Now, the total wages is

= (11x/15) ⋅ (25y/15)

= 5xy/6

So, the total wages after changes is

= 5xy/6 -----(2)

From (1) and (2) we get that the total wages get decreased from xy to 5xy/6.

So, the decrement  ratio is

= xy : 5xy/6

Divide both the terms by xy.

= 1 : 5/6

Multiply both the terms by 6.

= 6 : 5

Hence, the total wages will be decreased in the ratio

6 : 5

7. Answer :

Given ratio ---> 1/2 : 2/3 : 3/4.

First let us convert the terms of the ratio into integers.

L.C.M of denominators (2, 3, 4) = 12.

When we multiply each term of the ratio by 12, we get

12 ⋅ 1/2 : 12 ⋅ 2/3 : 12 ⋅ 3/4 ----> 6 : 8 : 9

From the ratio 6 : 8 : 9,

share of A = 6x

share of B = 8x

share of C = 9x

We know that,

share of A + share of B + share of C = 782

6x + 8x + 9x = 782

23x = 782

x = 34

Share of A is

= 6x

= 6 ⋅ 34

= 204

So, the share of A is $204.

8. Answer :

From the given ratio 3 : 7 : 12,

share of P = 3x

share of Q = 7x

share of R = 12x

Difference between the shares of P and Q is $ 2400.

share of Q - share of P = 2400

7x - 3x = 2400

4x = 2400

x = 600

Difference between the shares of Q and R is

= 12x - 7x

= 5x

= 5 ⋅ 600

= 3000

So, the difference between the shares of Q and R is $3000.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.