WORKSHEET ON
THEORETICAL PROBABILITY

Problem 1 :

A die is rolled. What is the theoretical probability of getting :

a) a "six"

b) a "prime number"?

Solution

Problem 2 :

A bag contains 1 yellow, 2 green and 5 blue beds. One bead is chosen at random. Find the probability that it is :

(a)  Yellow  (b)  not yellow

Solution

Problem 3 :

1 A die numbered 1 to 6 is rolled once. Find:

a) P(3)

b) P(even number)

c) P(a number at least 1)

d) P(5)

e) P(not a 5)

f) P(a number greater than 6)

Solution

Problem 4 :

The five illustrated cards are well shuffled and placed face down on a table. One of the cards is randomly chosen. 

Solution

Problem 5 :

A bag contains 10 beads. 5 are white, 2 are red, 1 is blue, 1 is green and 1 is black. A bead is taken at random from the bag. Find:

a) P(white)

b) P(blue)

c) P(not black)             Solution

Problem 6 :

A letter is randomly chosen from GENEVA.

a)  Find the probability that it is:

(i) an E

(ii) a Z

b) Given that the letter chosen first is a G and it is removed, what is the probability that a second randomly chosen letter is a vowel?          Solution

Problem 7 :

A dart board has 30 sectors, numbered 1 to 30. A dart is thrown towards the bulls-eye and misses in a random direction. Determine the probability that the dart hits:

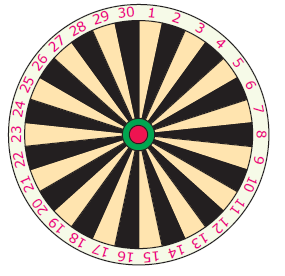
a) a multiple of 5

b) a number between 7 and 13 inclusive

c) a number greater than 18

d) 15

e) a multiple of 7

f) an even number that is a multiple of 3.

Solution

Problem 8 :

A shoebox holds a number of disks of the same size. There are 5 red, 6 white, and 7 blue disks. You pick out a disk, record its color, and return it to the box. If you repeat this process 250 times, how many times can you expect to pick either a red or white disk?

Solution

Problem 1 :

A standard number cube is rolled 150 times. Predict how many times it will roll a 3 or a 4.

Solution

Problem 2 :

Celia volunteers at her local animal shelter. She has an equally likely chance to be assigned to the dog, cat, bird, or reptile section. If she volunteers 24 times, about how many times should she expect to be assigned to the dog section ?

Solution

Problem 3 :

All 2,000 customers at a gym are randomly assigned a 3-digit security code that they use to access their online accounts. The codes are made up of the digits 0 through 4, and the digits can be repeated. Is it likely that fewer than 10 of the customers are issued the code 103 ?

Solution

Problem 4 :

Gill rolls a number cube 78 times. How many times can he expect to roll an odd number greater than 1?

Solution

Problem 5 :

Jenna flips two pennies 105 times. How many times can she expect both coins to come up heads?

Solution

Problem 6 :

Ron draws 16 cards from a deck of 52 cards. The deck is made up of cards of four different colors—red, blue, yellow, and green. How many of the cards drawn can Ron expect to be green?

Solution

Problem 7 :

A bag contains 6 red and 10 black marbles. If you pick a marble from the bag, what is the probability that the marble will be black?

Solution

Problem 8 :

A bag contains 6 red and 10 black marbles. If you pick a marble, record its color, and return it to the bag 200 times, how many times can you expect to pick a black marble?

Solution

Problem 9 :

Harriet rolls a number cube. What is the probability that the number cube will land on 3 or 4?

Solution

Problem 10 :

Harriet rolls a number cube. If he rolls the number cube 39 times, how many times can she expect to roll a 3 or 4?

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.