WORKSHEET ON SQUARE ROOT

1. Find the square root of 104976 by long division.

2. Simplify : √64 + √196

3. Simplify : 2√425 - 3√68

4. Simplify : (√17)(√51)

5. Simplify : (7√5)²

6. Simplify : (√3)³ + √27

7. If √a = 1/5, then find the value of a. 

8. If (√4)⁷ ⋅ (√2)^-4 = 2^k, then solve for k. 

9. The value of (√80 - √112)/(√45 - √63) is ?

10. If √1 + (55/729) = 1 + (x/27), then the value of x is :

a)  1     b)  3    c)  5    d)  7

11. √(0.081 x 0.324 x 4.624)/(1.5625 x 0.0289 x 72.9 x 64) is equal to 

a)  0.024    b)  0.24     c)  2.4    d)  24

12. The square root of (7 + 3√5) (7 - 3 √5) is

a)   √5       b)  2     c)  4     d)  3 √5

1. Answer :

Step 1 :

Separate the digits by taking commas from right to left once in two digits.

10,49,76  

When we do so, we get 10 before the first comma.

Step 2 :

Now we have to multiply a number by itself such that

the product ≤ 10

(The product must be greatest and also less than 10)

The above condition will be met by “3”.

Because 3 ⋅ 3  =  9  ≤  10.

Now this situation is explained using long division

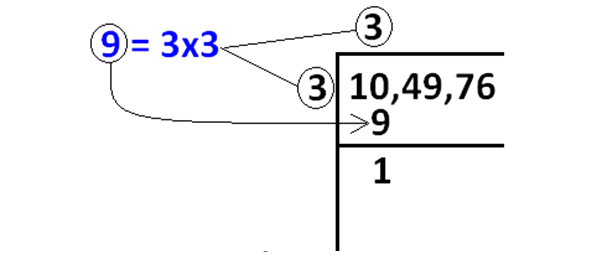
In the above picture, 9 is subtracted from 10 and we got the remainder 1.

Step 3 :

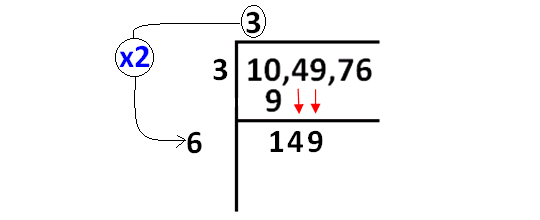
Now, we have to bring down 49 and quotient 3 to be multiplied by 2 as given in the picture below.

Step 4 :

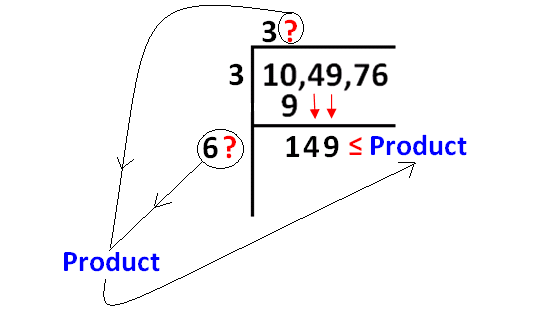
Now we have to take a same number at the two places indicated by "?".

Then, we have to find the product as shown in the picture and also the product must meet the condition as indicated.

Step 5 :

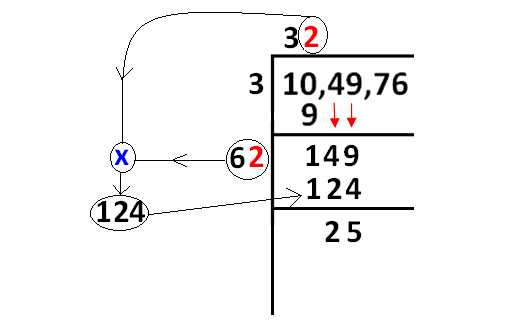
The condition said in step 4 will be met by replacing "?" with "2". 

Than we have to do the calculation as given in the picture.

Step 6 :

Now, we have to bring down 76 and quotient 32 to be multiplied by 2 as given in the picture below.

Step 7 :

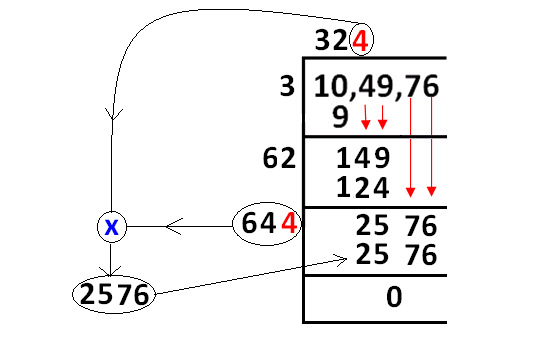
In the above picture, we have applied the procedures explained in step 4 and step 5. And we got the remainder zero.  

Step 8 :

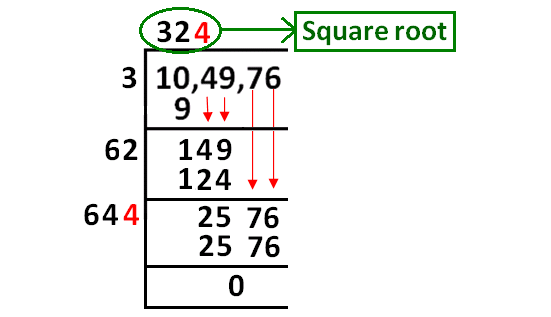
From the above picture, finally we got the square root of 104976. That is 324.

√104976 = 324

2. Answer

Because 64 and 196 are perfect squares, we can find the square root of 64 and 194 as shown below. 

√64 + √196 = 8 + 14

√64 + √196 = 22

3. Answer :

Decompose 425 and 68 into prime factors using synthetic division. 

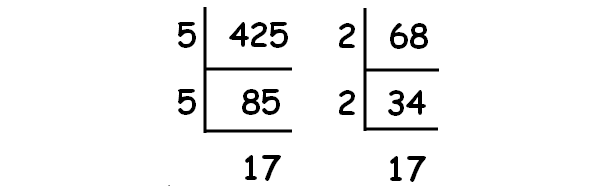
2√425 - 3√68 = 2(5√17) - 3(2√17)

= 10√17 - 6√17

= 4√17

4. Answer :

Decompose 17 and 51 into prime factors. 

Because 17 is a prime number, it can't be decomposed anymore. So, √17 has to be kept as it is. 

√51 = √(3 ⋅ 17) = √3 ⋅ √17

(√17)(√51) :

= (√17)(√3 ⋅ √17)

= (√17 ⋅ √17)√3

= 17√3

5. Answer :

(7√5)² = 7√5 ⋅ 7√5

 = (7 ⋅ 7)(√5 ⋅ √5)

= (49)(5)

= 245  

6.  Answer :

(√3)³ + √27 = (√3 ⋅ √3 ⋅ √3) + √(3 ⋅ 3 ⋅ 3)

= (3 ⋅ √3) + 3√3

= 3√3 + 3√3

= 6√3

7. Answer : 

√a = 1/5

a = (1/5)²

a = 1²/5²

a = 1/25

8. Answer : 

 (√4)⁷ ⋅ (√2)^-4 = 2^k

2⁷ ⋅ (2^1/2)^-4 = 2^k

2⁷ ⋅ 2^-2 = 2^k

2^{7 - 2} = 2^k

2⁵ = 2^k

k = 5

9. Answer : 

The value of (√80 - √112)/(√45 - √63) is ?

√80 = √2 x 2 x 2 x 2 x 5

= (2 x 2) √5

= 4√5

√112 = √2 x 2 x 2 x 2 x 7

= 2 x 2 √7

= 4√7

√45 = √(3 x 3 x 5)

= 3 √5

√63 = √(3 x 3 x 7)

= 3√7

Applying these values, we get

(√80 - √112)/(√45 - √63) = (4√5 - 4√7)/(3√5 - 3√7)

= 4(√5 - √7)/3(√5 - √7)

= 4/3

So, the answer is 4/3.

10. Answer : 

 √1 + (55/729) = 1 + (x/27)

Simplifying the L.H.S more,

= √1 + (55/729)

= √(729 + 55)/729

= √784/729

= 28/27

Witting as mixed fraction, we get

= 1 + 1/27

Comparing with 1 + (x/27), the value of x is 1.

11. Answer : 

√(0.081 x 0.324 x 4.624)/(1.5625 x 0.0289 x 72.9 x 64)

0.081 = 81/1000

0.324 = 324/1000

4.624 = 4624/1000

1.5625 = 15625/10000

0.0289 = 289/10000

72.9 = 729/10

√0.081 x 0.324 x 4.624

= √(81/100) x (324/1000) x (4624/1000)

81 = 9 x 9

324 = 18 x 18

4624 = 68 x 68

= (9 x 18 x 68)/10000

√(1.5625 x 0.0289 x 72.9 x 64)

1.5625 = 15625/10000 ==> 125 x 125 / 100 x 100

0.0289 = 289/10000 ==> 17 x 17 / 100 x 100

72.9 = 729/10 ==> 27 x 27/10

64 = 8 x 8

√(1.5625 x 0.0289 x 72.9 x 64) = (125 x 17 x 27 x 8)/ (100 x 10)

= (9 x 18 x 68)/10000 ⋅ 1000/(125 x 17 x 27 x 8)

= 0.024

12. Answer : 

The square root of (7 + 3√5) (7 - 3 √5) is

= √(7 + 3√5) (7 - 3 √5)

= √7² - (3√5)²

= √49 - 9(5)

= √49 - 45

= √4

= 2

So, the answer is 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.