WORKSHEET ON RATIONAL NUMBERS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problems 1-4 : Simplify.
Problem 1 :
(-2/3) + (-1/3)
Problem 2 :
(+2/5) + (+1/5)
Problem 3 :
(-4/5) + (+7/5)
Problem 4 :
(+5/9) + (-8/9)
Problem 5 :
Subtract 2.5 from 3.5 using a number line.
Problem 6 :
Subtract 1.5 from 4.5 using a number line.
Problem 7 :
Subtract -1.5 from 2.5.
Problem 8 :
Multiply -16 and -1/8.
Problem 9 :
Multiply 2 and -1/4.
Problem 10 :
Divide 2/3 by -7/6.
Problem 11 :
Divide 9/5 by 3.
Problem 12 :
Malachi hikes for 2.5 miles and stops for lunch. Then he hikes for 1.5 more miles. How many miles did he hike altogether?
Problem 13 :
During the day, the temperature increases by 4.5 degrees. At night, the temperature decreases by 7.5 degrees. What is the overall change in temperature?
Problem 14 :
During the hottest week of the summer, the water level of the Muskrat River was 5/6 foot below normal. The following week, the level was 1/3 foot below normal. What is the overall change in the water level ?
Problem 15 :
Gina hiked down a canyon and stopped each time she descended 1/2 mile to rest. She hiked a total of 4 sections. What is her overall change in elevation?
Problem 16 :
A diver needs to descend to a depth of 100 feet below sea level. She wants to do it in 5 equal descents. How far should she travel in each descent?

1. Answer :
(-2/3) + (-1/3)
Step 1 :
Find the absolute values.
|-2/3| = 2/3 and |-1/3| = 1/3
Step 2 :
Find the sum of the absolute values :
2/3 + 1/3 = (2 + 1)/3
= 3/3
= 1
Step 3 :
Use the sign of the rational numbers to write the sum.
(-2/3) + (-1/3) = -1
2. Answer :
(+2/5) + (+1/5)
Step 1 :
Find the absolute values.
|+2/5| = 2/5 and |+1/5| = 1/5
Step 2 :
Find the sum of the absolute values :
2/5 + 1/5 = (2 + 1)/5
2/5 + 1/5 = 3/5
Step 3 :
Use the sign of the rational numbers to write the sum.
(+2/5) + (+1/5) = +3/5
3. Answer :
(-4/5) + (+7/5)
Step 1 :
Find the absolute difference of the rational numbers without the actual signs.
|4/5 - 7/5| = |-3/5| = 3/5
Step 2 :
In the given two rational numbers 4/5 and 7/5, the sign of the bigger number is positive. So, we have to take positive sign to the answer.
So,
(-4/5) + (+7/5) = +3/5
4. Answer :
(5/9) + (-8/9)
Step 1 :
Find the absolute difference of the rational numbers without the actual signs.
|5/9 - 8/9| = |-3/9| = 3/9 = 1/3
Step 2 :
In the given rational numbers 5 and 8, the sign of the bigger number is negative. So, we have to take negative sign to the answer.
So,
(+5/9) + (-8/9) = -1/3
5. Answer :
Since we subtract a positive rational number 2.5 from 3.5, we have to move 2.5 units in the negative direction from 3.5 on the number line as given in the picture below.

After having moved 2.5 units in the negative direction, we are in the position of '1'.
So,
3.5 - (+2.5) = 1
6. Answer :
Since we subtract a positive rational number 1.5 from 4.5, we have to move 1.5 units in the negative direction from 4.5 on the number line as given in the picture below.
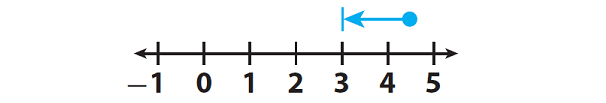
After having moved 1.5 units in the negative direction, we are in the position of '3'.
So,
4.5 - (+1.5) = 3
7. Answer :
Step 1 :
Since we subtract the negative rational number -1.5 from 2.5, we have to move 1.5 units from 2.5 in the positive direction on the number line.
It has been illustrated in the picture given below.
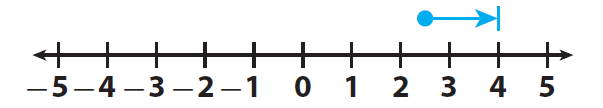
Step 2 :
After having moved 1.5 units in the positive direction from 2.5, we are in the position of '4'.
So,
2.5 - (-1.5) = 4
8. Answer :
Step 1 :
In the two rational numbers -16 and -1/8, the signs are same.
Step 2 :
Find the product of 16 and 1/8.
16 x 1/8 = 16/8 = 2
Step 3 :
Since we multiply two rational numbers with the same sign, the result is always positive.
So,
-16 x (-1/8) = 2
9. Answer :
Step 1 :
In the two rational numbers 2 and -1/4, the signs are different.
Step 2 :
Find the product of 2 and 1/4.
2 x 1/4 = 2/4 = 1/2
Step 3 :
Since we multiply two rational numbers with different signs, the result is always negative.
So,
2 x (-1/4) = -1/2
10. Answer :
Step 1 :
Take the reciprocal of the second rational number.
-7/6 ----> reciprocal ----> -6/7
Step 2 :
Multiply the first rational number 2/3 by -6/7
(2/3) x (-6/7)
Step 3 : Simplify
(2/1) x (-2/7)
Step 4 : Multiply
(2/1) x (-2/7) = -4/7
So,
2/3 ÷ -7/6 = -4/7
11. Answer :
Step 1 :
Take the reciprocal of the second rational number.
3 ----> reciprocal ----> 1/3
Step 2 :
Multiply the first rational number 9/5 by 1/3.
(9/5) x (1/3)
Step 3 : Simplify
(3/5) x (1/1)
Step 4 : Multiply
(3/5) x (1/1) = 3/5
So,
9/5 ÷ 3 = 3/5
12. Answer :
Step 1 :
Use positive numbers to represent the distance Malachi hiked.
Step 2 :
Find 2.5 + 1.5.
Let us use the real number line to add 2.5 and 1.5.
Step 3 :
Start at 2.5.
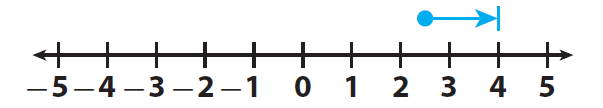
Step 4 :
Move 1.5 units to the right because the second addend is positive.
The result is 4.
So, Malachi hiked 4 miles.
13. Answer :
Step 1 :
Use a positive number to represent the increase in temperature and a negative number to represent a decrease in temperature.
Step 2 :
Find 4.5 + (-7.5).
Let us use the real number line to add 4.5 and (-7.5).
Step 3 :
Start at 4.5.
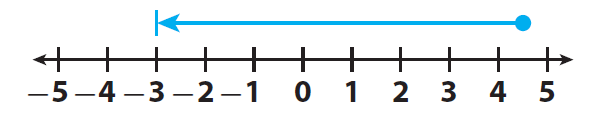
Step 4 :
Move | -7.5 | = 7.5 units to the left because the second addend is negative.
The result is -3.
So, the temperature decreased by 3 degrees overall.
14. Answer :
Subtract to find the difference in water levels. That is, we have to find -1/3 - (-5/6).
Step 1 :
Since we subtract the negative rational number -5/6 from -1/3, we have to move 5/6 units from -1/3 in the positive direction on the number line.
It has been illustrated in the picture given below.
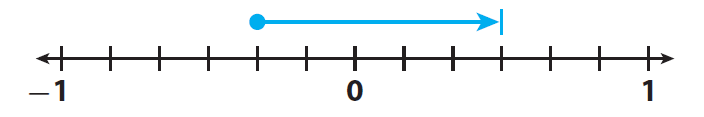
Step 2 :
After having moved 5/6 units in the positive direction from -1/3, we are in the position of '1/2'.
So, the water level changed 1/2 foot.
15. Answer :
Step 1 :
Use a negative number to represent the change in elevation.
Step 2 :
Find 4 x (-1/2).
Step 3 :
Start at 0. Move 1/2 unit to the left 4 times.

The result is -2.
Hence, the overall change is -2 miles.
Check :
Use the rules for multiplying rational numbers.
4 x (-1/2) = -4/2
4 x (-1/2) = -2
16. Answer :
To find how far she should travel in each descent, we have to divide 100 by 5.
Step 1 :
Take the reciprocal of the divisor 5.
5 ----> reciprocal ----> 1/5
Step 2 :
Multiply 100 by 1/5.
(100) x (1/5)
Step 3 : Simplify
(20) x (1/1)
Step 4 : Multiply
(20) x (1/1) = 20
So, she should travel 20 feet in each descent.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact US | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 39)
Dec 11, 25 05:59 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation

