WORKSHEET ON PROBABILITY

Question 1 :

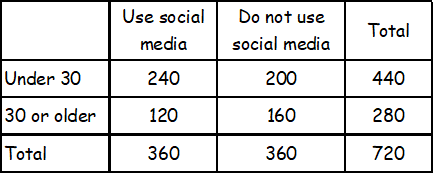
The table above shows the distribution of age and social media presence for 720 employees at a company. If an employee who uses social media is selected at random, what is the probability the employee is age 30 or older?

A) 1/3

B) 4/9

C) 1/2

D) 2/3

Question 2 :

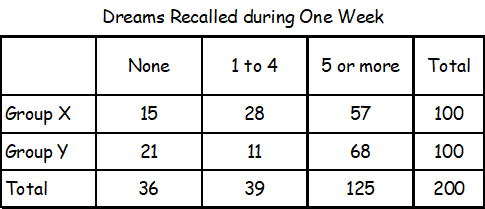
The data in the table above were produced by a sleep researcher studying the number of dreams people  recall when asked to record their dreams for one week. Group X consisted of 100 people who observed early bedtimes, and Group Y consisted of 100 people who observed later bedtimes. If a person is chosen at random from those who recalled at least 1 dream, what is the probability that the person belonged to Group Y?

A) 68/100

B) 79/100

C) 79/164

D) 164/200

Question 3 :

Results on the Bar Exam of Law School Graduates :

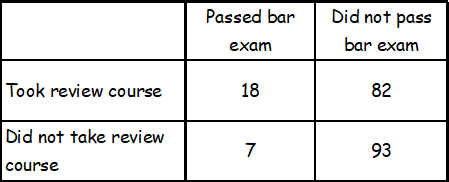
The table above summarizes the results of 200 law school graduates who took the bar exam. If one of the surveyed graduates who passed the bar exam is chosen at random for an interview, what is the probability that the person chosen did NOT take the review course?

A) 18/25

B) 7/25

C) 25/200

D) 7/200

Question 4 :

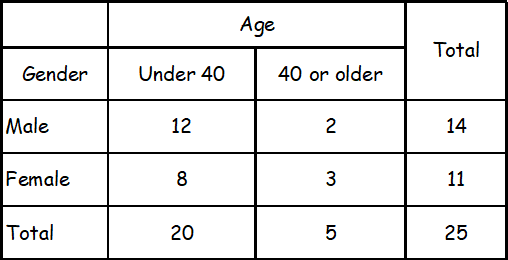
The table above shows the distribution of age and gender for 25 people who entered a contest. If the contest winner will be selected at random, what is the probability that the winner will be either a female under age 40 or a male age 40 or older?

A) 4/25

B) 10/25

C) 11/25

D) 16/25

Question 5 :

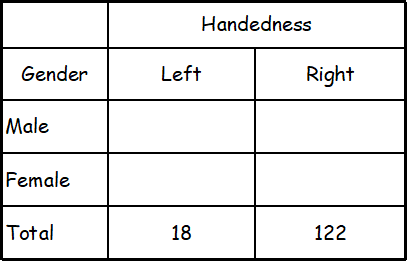
The incomplete table above summarizes the number of left-handed students and right-handed students by gender for the eighth-grade students at Keisel Middle School. There are 5 times as many right-handed female students as there are left-handed female students, and there are 9 times as many right-handed male students as there are left-handed male students. If there is a total of 18 left-handed students and 122 right-handed students in the school, which of the following is closest to the probability that a right-handed student selected at random is female? (Note: Assume that none of the eighth-grade students are both right-handed and left-handed.)

A) 0.410

B) 0.357

C) 0.333

D) 0.250

Question 6 :

Number of Registered Voters in the United States in 2012, in Thousands

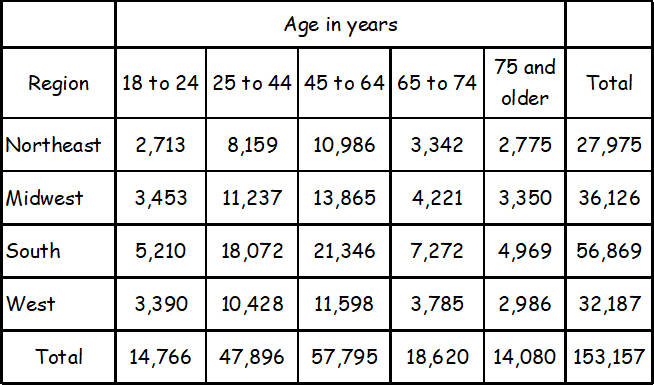
The table above shows the number of registered voters in 2012, in thousands, in four geographic regions and five age groups. Based on the table, if a registered voter who was 18 to 44 years old in 2012 is chosen at random, which of the following is closest to the probability that the registered voter was from the Midwest region?

A) 0.10

B) 0.25

C) 0.40

D) 0.75

Question 7 :

A coin is tossed twice. What is the probability of getting exactly one head ?

Question 8 :

Four coins are tossed once. What is the probability of getting at least 2 heads ?

Question 9 :

A card is drawn at random from a well shuffled pack of 52 cards. What is the probability that the card is neither a spade nor a Jack ?

Question 10 :

Two dice are thrown simultaneously. Find the probability that the sum of points on the two dice would be 7 or more.

1. Answer :

Required Probability :

The correct answer choice is (A).

2. Answer :

Recalled at least 1 dream means minimum 1 dream to the maximum number of dreams.

Total number of persons who recalled at least 1 dream :

= 39 + 125

= 164

Number of persons who recalled at least 1 dream belonging to group Y :

= 11 + 68

= 79

Required Probability :

The correct answer choice is (C).

3. Answer :

Required Probability :

The correct answer choice is (B).

4. Answer :

Of the 25 people who entered the contest, there are 8 females under age 40 and 2 males age 40 or older.

The probability that the contest winner will be either a female under age 40 or a male age 40 or older :

= P(female under age 40 or a male age 40 or older)

= (8 + 2)/25

= 10/25

The correct answer choice is (B).

5. Answer :

Let x be the number of left-handed female students and let y be the number of left-handed male students.

Given : Number of right-handed female students is 5 times the number of left-handed female students, and number of right handed male students is 9 times the number of left-handed male students.

Number of right handed female students = 5x

Number of right handed male students = 9y

From the table above,

x + y = 18 ----(1)

5x + 9y = 122 ----(2)

-9(1) + (2) :

-4x = -40

Divide both sides by -4.

x = 10

Number of right handed female students :

= 5x

= 5(10)

= 50

Required probability :

The correct answer choice is (A).

6. Answer :

From the table given, in 2012, total registered voters between 18 and 44 years old :

= 14,766 + 47,896

= 62,662

Total registered voters between 18 and 44 years old from the Midwest region :

= 3,453 + 11,237

= 14,690

The probability that a randomly chosen registered voter who was between 18 and 44 years old in 2012 was from Midwest region :

= 14,690/62,666

≈ 0.234

Of the given choices, 0.25 is closest to 0.234.

The correct answer choice is (B).

7. Answer :

When a coin is tossed twice, total number of all possible outcomes :

= 2 x 2

= 4

Sample space :

S = {HH, TT, HT, TH}

n(S) = 4

Letting A be the event of getting exactly one head.

A = {HT, TH}

n(A) = 2

Required probability :

P(A) = n(A)/n(S)

= 2/4

= 0.50 or 50%

8. Answer :

When four coins are tossed once, total no. of all possible outcomes :

= 2 x 2 x 2 x 2

= 16

Sample space :

S = {HHHH, TTTT, HHHT, HHTH, HTHH, THHH, TTTH, TTHT, THTT, HTTT, HHTT, TTHH, HTHT, THTH, HTTH, THHT}

n(S) = 16

Let A be the event of getting at least two heads.

Then A has to include all the events in which there are two heads and more than two heads. 

A = {HHHH, HHHT, HHTH, HTHH, THHH, TTHH, HHTT, THTH, HTHT, THHT, HTTH}

n(A) = 11

Required probability :

P(A) = n(A)/n(S)

= 11/16

9. Answer :

Let A be the event of drawing a card that is neither spade nor Jack. 

There are 13 spade cards in a pack of 52 cards. 

(Jack in spade is already included in these 13 cards)

In the remaining 3 types (club, heart, diamond), there are 3 jack cards. 

Number of spade cards and jack cards :

= 13 + 3

= 16 

So, number of cards which are neither spade nor Jack :

= 52 - 16

= 36

n(A) = 36

And also

n(S) = 52

Required probability :

P(A) = n(A) / n(S)

= 36/52

= 9/13

10. Answer :

If two dice are thrown then, as explained in the last problem, total no. of elementary events is 62 or 36.

Now a total of 7 or more i.e. 7 or 8 or 9 or 10 or 11 or 12 can occur only in the following combinations :

sum = 7 ----> (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)

sum = 8 ----> (2, 6), (3, 5), (4, 4), (5, 3), (6, 2)

sum = 9 ----> (3, 6), (4, 5), (5, 4), (6, 3)

sum = 10 ----> ((4, 6), (5, 5), (6, 4)

sum = 11 ----> (5, 6), (6, 5)

sum = 12 ----> (6, 6)

Thus the number of favorable outcomes is 21.

Letting A stand for getting a total of 7 points or more, we have

P(A) = 21/36

= 7/12

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.