WORKSHEET ON PARABOLAS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
The graph of a parabola in the xy-plane has x-intercepts -1/5 and 3/2. Which of the following could be the equation of the parabola?
A) y = (5x - 1)((2x + 3)
B) y = (5x + 1)(2x - 3)
C) y = (5x - 3)(2x + 1)
D) y = (5x + 3)(2x - 1)
Question 2 :
y = x2 - 2x - 3
A parabola in the xy-plane is given by the equation above. Which of the following equivalent forms of the equation displays the coordinates of the vertex of parabola as constants or coefficients?
A) y = (x - 1)2 - 4
B) y = (x - 1)2 - 2
C) y = (x - 3)(x + 1)
D) y + 3 = x(x + 2)
Question 3 :
y = x2 + 10x + 16
The equation above represents a parabola in the xy-plane. Which of the following equivalent forms of the equation displays the minimum values of y as a constant or coefficient?
A) y = (x + 8)(x + 2)
B) y - 16 = x(x + 10)
C) y = (x + 5)2 - 9
D) y = (x - 5)2 + 9
Question 4 :
y = x2 - 10x + k
In the equation above, k is a constant. If the equation represents a parabola in the xy-plane that is tangent to the x-axis, what is the value of k?
Question 5 :
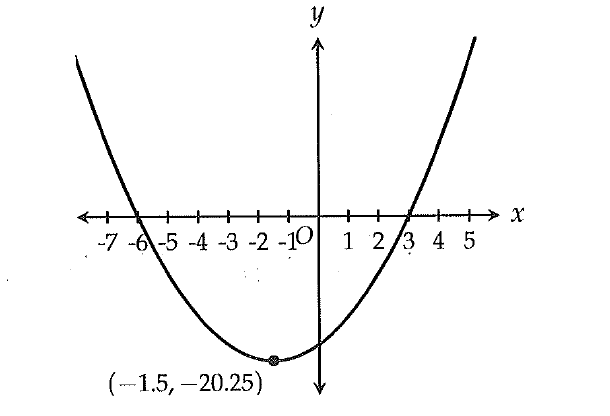
A parabola is shown in the xy-plane above. Which of the following equations correctly represents the parabola by displaying the x-intercepts of the parabola as constants or coefficients?
A) y = (x + 1.5)2 - 20.25
B) y = (x - 1.5)2 - 20.25
C) y = (x + 6)(x - 3)
D) y = (x - 6)(x + 3)
Question 6 :
h = -4.9t2 + 40t
The equation above expresses the height h, in meters, of an object t seconds after it is thrown into the air from the ground with an initial speed of 40 meters per second. After approximately how many seconds will the object reach its highest point?
A) 3
B) 4
C) 5
D) 6

1. Answer :
To find x-intercepts of any curve, we have to plugin y = 0 into its equation and find the values of x.
In each of the answer choices, plugin y = 0 and find x-intercepts.
A) y = (5x - 1)((2x + 3) :
(5x - 1)((2x + 3) = 0
5x - 1 = 0 or 2x + 3 = 0
x = 1/5 or x = -3/2
x-intercepts are 1/5 and -3/2.
B) y = (5x + 1)((2x - 3) :
(5x + 1)((2x - 3) = 0
5x + 1 = 0 or 2x - 3 = 0
x = -1/5 or x = 3/2
x-intercepts are -1/5 and 3/2.
C) y = (5x - 3)(2x + 1) :
(5x - 3)((2x + 1) = 0
5x - 3 = 0 or 2x + 1 = 0
x = 3/5 or x = -1/2
x-intercepts are 3/5 and -1/2.
D) y = (5x + 3)(2x - 1) :
(5x + 3)((2x - 1) = 0
5x + 3 = 0 or 2x - 1 = 0
x = -3/5 or x = 1/2
x-intercepts are -3/5 and 1/2.
The correct answer choice is (B).
2. Answer :
The vertex form equation of a parabola y = a(x - h)2 + k, displays the coordinates of the vertex (h, k) as constants or coefficients.
Write the given equation of the parabola in vertex form using completing the square method.
y = x2 - 2x - 3
y = x2 - 2(x)(1) - 3
y = x2 - 2(x)(1) + 12 - 12 - 3
Using the algebraic identity, (a + b)2 = a2 + 2ab + b2,
y = (x - 1)2 - 12 - 3
y = (x - 1)2 - 1 - 3
y = (x - 1)2 - 4
The correct answer choice is open (A).
3. Answer :
The minimum or maximum value of y in a parabola is the y-coordinate at the vertex.
If the parabola opens up, we have minimum value for y and if the parabola opens down and we have maximum value for y.
When the equation of a parabola is given and if you want to find the minimum value of y, then write the given equation of the parabola in vertex form.
The vertex form equation of a parabola is y = a(x - h)2 + k, where (h, k) is the vertex. When a > 0, the parabola opens down and the minimum value of y is k.
y = x2 + 10x + 16
y = x2 + 2(x)(5) + 16
y = x2 + 2(x)(5) + 52 - 52 + 16
Using the algebraic identity, (a + b)2 = a2 + 2ab + b2,
y = (x + 5)2 - 52 + 16
y = (x + 5)2 - 25 + 16
y = (x + 5)2 - 9
The correct answer choice is open (C).
4. Answer :
If a parabola is tangent to the x-axis, its equation has only one solution when y = 0.
x2 - 10x + k = 0
Since the above equation has only one solution, the value of the discriminant b2 - 4ac must be zero.
Comparing ax2 + bx + c = 0 and x2 - 10x + k = 0,
a = 1, b = -10 and c = k
b2 - 4ac = 0
(-10)2 - 4(1)k = 0
100 - 4k = 0
-4k = -100
k = 25
5. Answer :
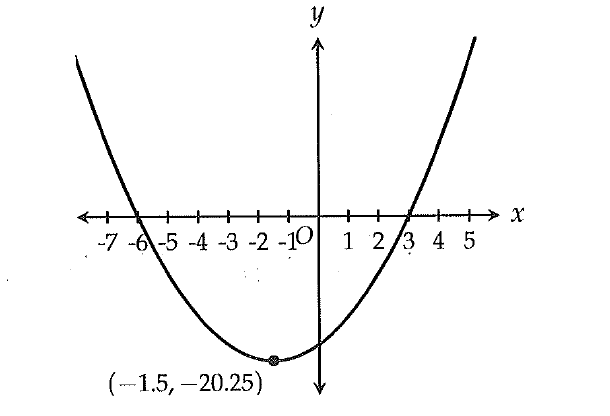
From the graph, the two x-intercepts are -6 and 3.
The corresponding factors of the two x-intercepts -6 and 3 are (x + 6) and (x - 3) respectively.
Answer (C) is the only one with both of these factors.
The correct answer choice is (C).
6. Answer :
Since h = -4.9t2 + 40t is a quadratic equation, the path of the object is a parabola.
A parabola with the equation y = ax2 + bx + c has its maximum or minimum at x = -b/2a.
Comparing y = ax2 + bx + c and h = -4.9t2 + 40t,
a = -4.9, b = 40 and c = 0
In h = -4.9t2 + 40t, since the leading coefficient of h is negative (-4.9), the parabola opens down and h has its maximum value at
t = -b/2a
Substitute b = 40 and a = -4.9.
t = -40/2(-4.9)
t ≈ -40/(-9.8)
t ≈ 4.08
Therefore,
the object reaches its highest point about
4 seconds after it is thrown.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
