WORKSHEET ON MARKUP AND MARKDOWN

1. A computer store used a markup rate of 40%. Find the selling price of a computer game that cost the retailer $25.

2. A store uses a 40% markup on cost. Find the cost of a pair of shoes that sells for $63.

3. A product that regularly sells for $425 is marked down to $318.75. What is the discount rate?

4. A trader cheats his customer to make a profit by stating that he sells at cost price but gives his customers only 800 grams. for every 1000 grams. What is the mark up rate?

5. Mr. Lenin sold a chair at a loss of 15%. If he had sold at a mark up rate of 10%, he would have got $100 more. What is the cost price of the chair? 

6. I purchased 120 books at the rate of $3 each and sold 1/3 of them at the rate of $4 each. 1/2 of them at the rate  of $ 5 each and rest at the cost price. Find my profit percentage.  

7. A trader marks his goods 20% above the cost price and allows a discount of 10% for cash. Find the mark up rate.

8. A person buys 8 articles for $15 and sells them at 10 for $18. Find the gain or loss percentage. 

9. Sum of the cost price of two products is $50. Sum of the selling price of the same two products is $52. If one is sold at 20% and other one is sold at 20% loss, find the cost price of each product.  

10. On selling an item, a trader gets a profit of $20. If the selling price is five times the profit, find the mark up rate. 

1. Answer :

Selling price = (100 + m)% ⋅ C . P

Substitute m = 40 and C. P = $25.

= (100 + 40)% ⋅ 25

= 140% ⋅ 25

= 1.4 ⋅ 25

= $35

2. Answer : 

S. P = (100 + m)% ⋅ Cost price

Cost price = S. P/(100 + m)%

Substitute S. P = 63 and m = 40.

Cost price = 63/(100 + 40)%

= 63/140%

 = 63/1.4

= $45

3. Answer : 

Regular price = $ 425

Marked down price = $ 318.75

Marked down value = 425 - 318.75 = 106.25

Marked down rate = (106.25/425) ⋅ 100%

= 25%

4. Answer :

Cheated Value = 1000 - 800 = 200

False weight = 800

Mark up rate = (Cheated value/False weight) ⋅ 100%

Mark up rate = (200/800) ⋅ 100%

= 25%

5. Answer :

Let x be the cost price of the chair.

S. P (-15%) = 85% of x

S. P (-15%) = 0.85x ----(1)

S. P (+10%) = 110% of x

      S. P (+10%) = 1.1x ----(2)

In (2), he got $100 more than (1).

(2) - (1) = 100

1.1x - 0.85x = 100

0.25x = 100

Divide each side by 0.25.

x = 400

The cost price of the chair is $400.

6. Answer :

Total money invested = 120 ⋅ 3 = $360 ----(1)

Let us see, how 120 books are sold in different prices.

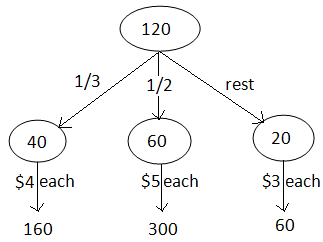
From the above picture,

Total money received = 160 + 300 + 60 = $520 ----(2)

Profit = (2) - (1)

= 520 - 360

= $160

Mark up rate = (160/360) ⋅ 100%

= 44.44%

7. Answer :

Let the cost price be $100. 

Then, marked price  is $120.

Let x be the selling price. 

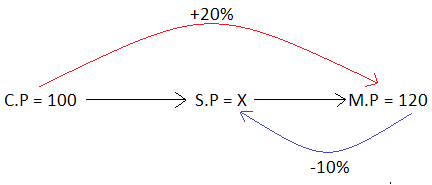
From the above picture, we get

90% of (M. P) = x

0.9 ⋅ 120 = x

108 = x

Therefore, the selling price is $108.

Cost price = $100

Selling Price = $108

Mark up rate = 8%

8. Answer :

Given : A person buys 8 articles for $15 and sells them at 10 for $18. 

Find the least common multiple of 8 and 10. 

The least common multiple of 8 and 10 is 40. 

Find both cost price and selling price for 40 articles. 

Cost price :

8 articles -----> $15 

40 articles = 5 ⋅ 8 articles = 5 ⋅ 15 = $75

C. P of 40 articles = $75 -----(1)

Selling price :

10 articles -----> $18

40 articles = 4 ⋅ 10 articles = 4(18) = $72

S. P of 40 articles = $72 -----(2)

From (1) and (2), the cost price is more than the selling price. 

That is, C. P > S. P. So, there is loss.

Loss = (1) - (2)

= 75 - 72

= 3

Loss percentage = (3/75) ⋅ 100%

= 4%

9. Answer :

Let x and y be the cost prices of two products. 

x + y = 50 ----(1)

Let us assume that x is sold at 20% profit.

The selling price of x is 

= 120% ⋅ x

= 1.2x

Let us assume that y is sold at 20% loss.

The selling price of y is

= 80% ⋅ y

= 0.8y

Given : Sum of the selling prices of x and y is $52.

1.2x + 0.8y = 52

Multiply each side 10.

12x + 8y = 520

Divide each side by 4. 

3x + 2y = 130 ----(2)

Solving (1) and (2), we get .

x = 30

y = 20 

So, the cost prices of the two products are $30 and $20.

10. Answer :

Given : Profit is $20 and selling price is five times the profit. 

Selling price : 

= 5 ⋅ profit

= 5 ⋅ 20

= $100

Cost price :

= Selling price - Profit

= 100 - 20 

= $80

Profit : 

= Selling price - Cost price

= 100 - 80

= $20

Mark up rate :

= (profit/cost) ⋅ 100%

= (20/80) ⋅ 100%

= (1/4) ⋅ 100%

= 25%

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.