WORKSHEET ON LOCUS

Problem 1 :

Draw point C on a piece of paper.  Draw and describe the locus of all points on the paper that are e inches from c.

Problem 2 :

Points A and B lie in a plane.  What is the locus of points in the plane that are equidistant from points A and B and are a distance of AB from B ?

Problem 3 : 

Point P is in the interior of ∠ABC.  What is the locus of points in the interior of ∠ABC that are equidistant from both sides of ∠ABC and 2 inches form P ?  How does the location of P within ∠ABC affect the locus ?

Problem 4 :

We have the following readings of an earthquake from three seismographs.

(i)  At A(-5, 5), the epicenter is 4 miles away.

(ii)  At B(-4, -3.5), the epicenter is 5 miles away.

(iii)  At C(1, 1.5), the epicenter is 7 miles away.

Where is the epicenter ?

Answers

Problem 1 :

Draw point C on a piece of paper.  Draw and describe the locus of all points on the paper that are e inches from c.

Solution :

Step 1 : 

Draw point C. Locate several points e inches from C.

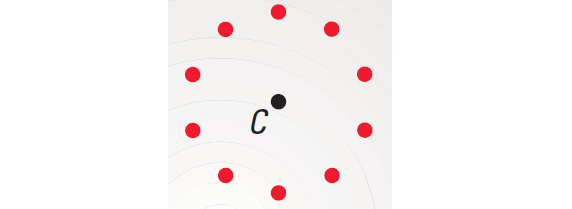
Step 2 :

Recognize a pattern: the points lie on a circle.

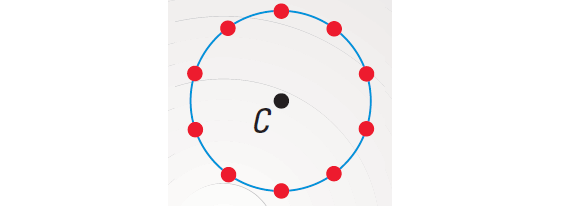
Step 3 :

Draw the circle using compass as shown below. 

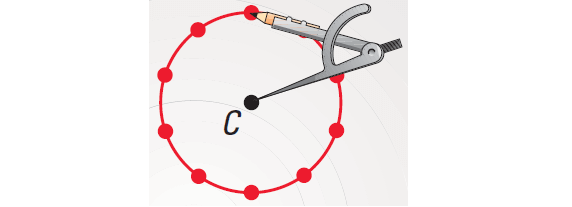
The locus of points on the paper that are e inches from C is a circle with center C and a radius of  3 inches.

Problem 2 :

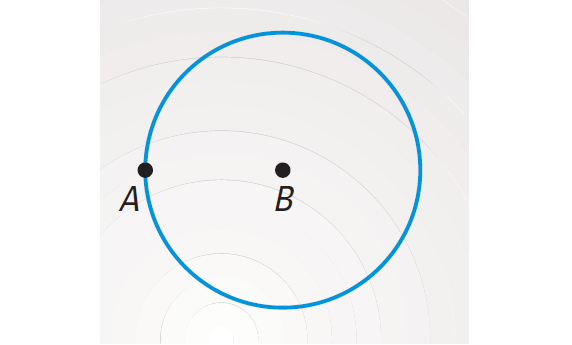
Points A and B lie in a plane.  What is the locus of points in the plane that are equidistant from points A and B and are a distance of AB from B ?

Solution :

The locus of all points that are equidistant from A and B is the perpendicular bisector of AB as shown below.

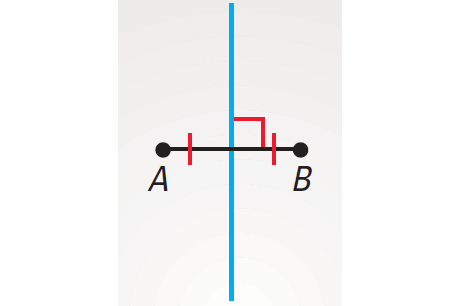
The locus of all points that are a distance of AB from B is the circle with center B and radius AB as shown below.

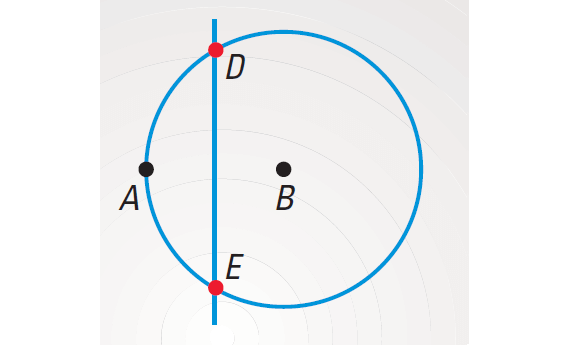
These loci intersect at D and E.  So D and E are the locus of points that satisfy both conditions.

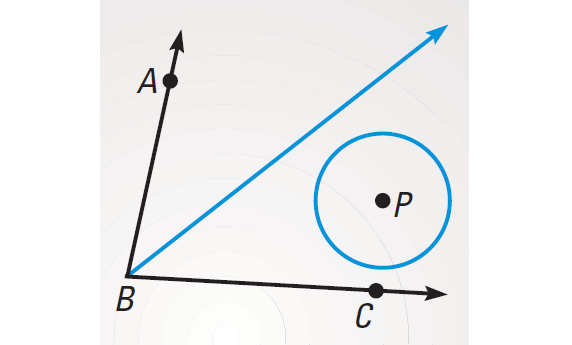
Problem 3 : 

Point P is in the interior of ∠ABC.  What is the locus of points in the interior of ∠ABC that are equidistant from both sides of ∠ABC and 2 inches form P ?  How does the location of P within ∠ABC affect the locus ?

Solution :

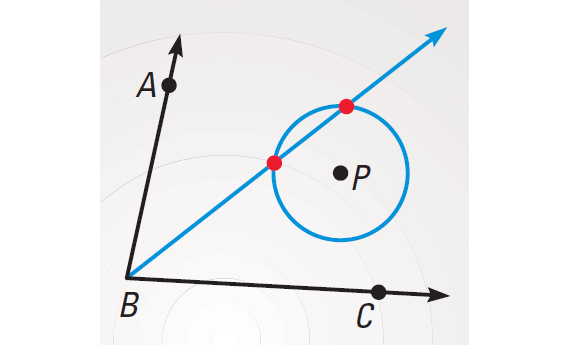
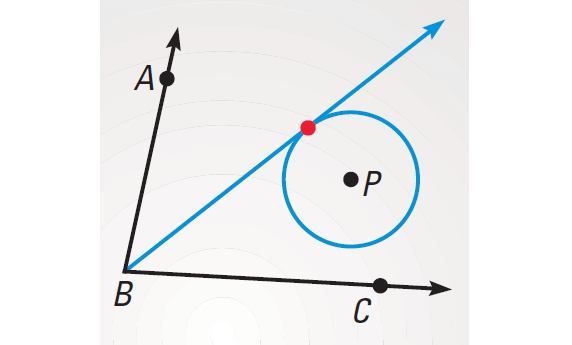
The locus of points equidistant from both sides of ∠ABC is the angle bisector.  The locus of points 2 inches form P is a circle.  The intersection of the angle bisector and the circle depends on the location of P. The  locus can be 2 points, 1 point, or 0 points.

The locus is two points :

The locus is one point :

The locus is zero points :

Problem 4 :

We have the following readings of an earthquake from three seismographs.

(i)  At A(-5, 5), the epicenter is 4 miles away.

(ii)  At B(-4, -3.5), the epicenter is 5 miles away.

(iii)  At C(1, 1.5), the epicenter is 7 miles away.

Where is the epicenter ?

Solution :

Each seismograph gives us a locus that is a circle.

So, we have

           Circle A has center (-5, 5) and radius 4

           Circle B has center (-4, -3.5) and radius 5

           Circle C has center (1, 1.5) and radius 7

Draw the three circles in a coordinate plane. The point of intersection of the three circles is the epicenter.

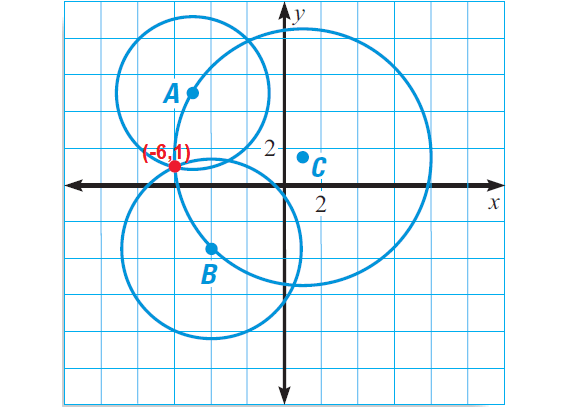
In the diagram above, three circles intersect at (-6, 1).

The epicenter is at about (-6, 1).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.