WORD PROBLEMS WITH SOLUTION IN VECTOR

Problem 1 :

If a vector and b vector represent a side and a diagonal of a parallelogram, find the other sides and the other diagonal.

Solution :

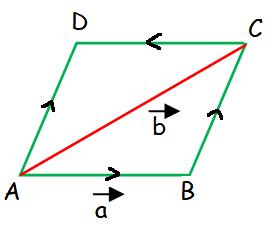
AB vector  =  a vector, AC vector  =  b vector

AB vector + BC vector  =  AC vector

BC vector  =  AC vector - AB vector

BC vector  =  b vector - a vector

The sides AB and CD are in opposite direction.

CD vector  =  -AB vector  =  -a vector

CD vector  =  - a vector

AD vector  =  b vector - a vector

To find the length of DA, we have to multiply AD vector by negative.

- AD vector  =  -(b vector - a vector)

DA vector  =  a vector - b vector

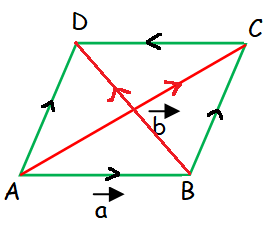
Now let us find the length of other diagonal BD.

AB vector + BD vector  =  AD vector

BD vector  =  AD vector - AB vector

  =  b vector - a vector - a vector

BD vector  =  b vector - 2a vector

Problem 2 :

If PO vector + OQ vector  = QO vector +OR vector, prove that the points P, Q, R are collinear.

Solution :

PO vector + OQ vector  = QO vector +OR vector

-OP vector + OQ vector  =  -OQ vector + OR vector

OQ vector - OP vector  =  OR vector - OQ vector

PQ vector  =  QR vector

Because they are equal, they are parallel and they have a common point Q.

So, the points P, Q and R are collinear.

Problem 3 :

If D is the midpoint of the side BC of a triangle ABC, prove that AB vector + AC vector = 2AD vector.

Solution :

From the given information, let us draw a rough diagram.

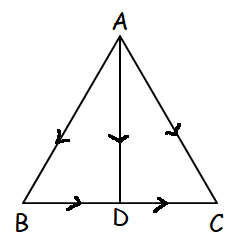
In triangle ABD,

AB vector + BD vector  =  AD vector

AB vector  =  AD vector - BD vector  ---(1)

In triangle ADC,

AD vector + DC vector  =  AC vector

AC vector  =  AD vector + DC vector  ----(2)

(1) + (2)

AB vector + AC vector  =  AD vector - BD vector + AD vector + DC vector

 AB vector + AC vector = 2AD vector - BD vector + DC vector. Since BD and DC are in same magnitude, they will get canceled.

 AB vector + AC vector = 2AD vector

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.