SOLVING WORD PROBLEMS INVOLVING QUADRATIC EQUATIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
If the difference between a number and its reciprocal is ²⁴⁄₅, find the number.
Solution :
Let x be the required number. Then its reciprocal is ¹⁄ₓ be its reciprocal.
5(x2 - 1) = 24x
5x2 - 5 = 24x
5x2 - 24x - 5 = 0
5x2 - 25x + 1x - 5 = 0
5x(x - 5) + 1(x - 5) = 0
(5x + 1)(x - 5) = 0
5x + 1 = 0 or x - 5 = 0
x = -⅕ or x = 5
So, the required number is -⅕ or -5.
Problem 2 :
A garden measuring 12m by 16m is to have a pedestrian pathway that is w meters wide installed all the way around so that it increases the total area to 285 m2. What is the width of the pathway?
Solution :
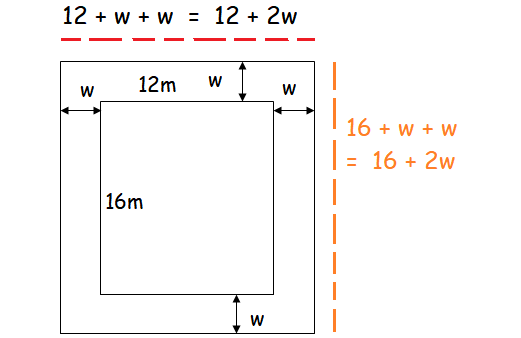
From the picture above, length of the garden including pathway is (12 + 2w) and width is (16 + 2w).
Total Area = 285 m2
Length ⋅ Width = 285
(12 + 2w)(16 + 2w) = 285
192 + 24w + 32w + 4w2 = 285
4w2 + 56w + 192 - 285 = 0
4w2 + 56w - 93 = 0
Solve the above quadratic equation using quadratic formula.
w = -15.5 or w = 1.5
Since w is the width of the pathway, it can not be negative. So, w = 1.5.
Therefore , the width of the pathway is 1.5 m.
Problem 3 :
A bus covers a distance of 90 km at a uniform speed. Had the speed been 15 km/hr more, it would have taken 30 minutes less for the journey. Find the original speed of the bus.
Solution :
Distance covered = 90 km
Let x be the original speed of the bus.
Increased speed = x + 15
Time taken by the bus in original speed :
= ⁹⁰⁄ₓ
Time taken by the bus in increased speed :
= ⁹⁰⁄₍ₓ ₊ ₁₅₎
From the given information, the difference between and ⁹⁰⁄ₓ and ⁹⁰⁄₍ₓ ₊ ₁₅₎ is 30 minutes or ½ hour.
2700 = x2 + 15x
x2 + 15x - 2700 = 0
x2 + 60x - 45x - 2700 = 0
x(x + 60) - 45(x + 60) = 0
(x - 45)(x + 60) = 0
x = 45 or x = -60
Since x represents the original speed of the bus, it can never be negative. So, x = 45.
Therefore, the original speed of the bus is 45 km per hour.
Problem 4 :
John and Jivanti together had 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they have now is 124. Find the number marbles each one them had initially.
Solution :
Let x be the number of marbles that john has.
Then, the number of marbles that Jivanthi has
= 45 - x
After losing 5 marbles,
number of marbles with John = x - 5
number of marbles with Jivanti = 45 - x - 5 = 40 - x
The product of number of marbles = 124
(x - 5)(40 - x) = 124
40x - x2 - 200 + 5x = 124
45x - x2 - 200 = 124
x2 - 45x + 124 + 200 = 0
x2 - 45x + 324 = 0
x2- 36x - 9x + 324 = 0
x(x - 36) - 9(x - 36) = 0
(x - 9)(x - 36) = 0
x - 9 = 0 or x - 36 = 0
x = 9 or x = 36
If x = 9,
= 45 - x
= 45 - 9
= 36
If x = 36,
= 45 - x
= 45 - 36
= 9
So, John had 36 marbles, when Jivanti had 9 marbles or Jivanti had 36 marbles, when John had 9 marbles.
Problem 5 :
A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in dollars) was found to be 55 minus the number of toys produced in a day, the total cost of production was $750. Find the number of toys produced on that day.
Solution :
Let x be the number of toys produced in a particular day.
Cost of production of one toy (in dollars) :
= 55 - x
Total cost = Number of toys ⋅ Cost of one toy
750 = x (55 - x)
750 = 55x - x2
x2 - 55x + 750 = 0
x2 - 30x - 25x + 750 = 0
x(x - 30) - 25(x - 30) = 0
(x - 30)(x - 25) = 0
x - 30 = 0 or x - 25 = 0
x = 30 or x = 25
So, the number of toys produced on that particular day is 30 or 25.
Problem 6 :
The diagonal of a rectangular field is 60 meters more than the shorter side. If the longer side is 30 meters more than the shorter side, find the sides of the field.
Solution :
Let x be the length of shorter side of the rectangle
Then,
length of diagonal = x + 60
length of longer side = x + 30
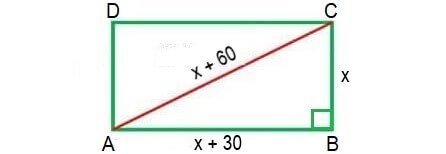
Using Pythagorean Theorem in the right triangle ABC,
(x + 60)2 = x2 + (x + 30)2
x2 + 602 + 2(x)(60) = x2 + x2 + 2(x)(30) + 302
x2 + 3600 + 120x = 2x2 + 60x + 900
2x2 - x2 + 60x - 120x + 900 - 3600 = 0
x2 - 60x - 2700 = 0
x2 - 90x + 30x - 2700 = 0
x(x - 90) + 30(x - 90) = 0
(x + 30)(x - 90) = 0
x + 30 = 0 or x - 90 = 0
x = -30 or x = 90
Because x represents breadth of the rectangle, it can never be negative. So, x = 90.
Therefore,
length of the shorter side = 90 m
length of the longer side = 90 + 30 = 120 m
Problem 7 :
The difference of squares of two positive numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
Solution :
Let x be the larger number and y be the smaller number.
The square of the smaller number is 8 times the larger number.
y2 = 8x -----(1)
The difference of squares of two numbers is 180.
x2 - y2 = 180
Substitute y2 = 8x and solve for x.
x2 - 8x = 180
x2 - 8x - 180 = 0
x2 - 18x + 10x - 180 = 0
x(x - 18) + 10(x - 18) = 0
(x - 18)(x + 10) = 0
x - 18 = 0 or x + 10 = 0
x = 18 or x = -10
Because the numbers are positive, x = -10 can not be accepted. So, x = 18.
Substitute x = 18 into (1).
y2 = 8(18)
y2 = 144
y = √144
y = 12
Therefore, the larger number is 18 and the smaller number is 12.
Problem 8 :
A train travels 360 miles at a uniform speed. If the speed had been 5 miles/hr more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution :
Distance covered = 360 miles
Let x be the original speed of the train.
If the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey.
Increased speed = x + 5
Time taken by the train in original speed :
= ³⁶⁰⁄ₓ
Time taken by the train in increased speed :
= ³⁶⁰⁄₍ₓ ₊ ₅₎
From the given information, the difference between and ³⁶⁰⁄ₓ and ³⁶⁰⁄₍ₓ ₊ ₅₎ is 1 hour.
1800 = x2 + 5x
x2 + 5x - 1800 = 0
x2 - 40x + 45x - 1800 = 0
x(x - 40) + 45(x - 40) = 0
(x - 40)(x + 45) = 0
x - 40 = 0 or x + 45 = 0
x = 40 or x = -45
Since x represents the original speed of the train, it can never be negative. So, x = 40.
Therefore, the original speed of the train is 40 miles/hr.
Problem 9 :
Find two consecutive positive even integers whose squares have the sum 340.
Solution :
Let x and (x + 2) be the two positive even integers.
Sum of their squares = 340
x2 + (x + 2)2 = 340
x2 + (x + 2)(x + 2) = 340
x2 + x2 + 2x + 2x + 4 = 340
2x2 + 4x + 4 = 340
2x2 + 4x - 336 = 0
Divide both sides by 2.
x2 + 2x - 168 = 0
Solve by factoring.
x2 - 12x + 14x - 168 = 0
x(x - 12) + 14(x - 12) = 0
(x - 12)(x + 14) = 0
x - 12 = 0 or x + 14 = 0
x = 12 or x = -14
Since the integers are positive, x can not be negative.
So,
x = 12
x + 2 = 14
Therefore, the two positive even integers are 12 and 14.
Problem 10 :
The sum of squares of three consecutive natural numbers is 194. Determine the numbers.
Solution :
Let x, x + 1 and x + 2 be three consecutive natural numbers.
Sum of their squares = 194
x2 + (x + 1)2 + (x + 2)2 = 194
x2 + (x + 1)(x + 1) + (x + 2)(x + 2) = 194
x2 + x2 + x + x + 1 + x2 + 2x + 2x + 4 = 194
3x2 + 6x + 5 = 194
3x2 + 6x - 189 = 0
Divide both sides by 3.
x2 + 2x - 63 = 0
Solve by factoring.
x2 - 7x + 9x - 63 = 0
x(x - 7) + 9(x - 7) = 0
(x - 7)(x + 9) = 0
x - 7 = 0 or x + 9 = 0
x = 7 or x = -9
Since the numbers are natural numbers, x can not be negative.
So,
x = 7
x + 1 = 8
x + 2 = 9
Therefore, the three consecutive natural numbers are 7, 8 and 9.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
US Common Core K-12 Curriculum Algebra Word Problems
Dec 20, 25 01:19 AM
US Common Core K-12 Curriculum Algebra Word Problems on Systems of LInear Equations -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Dec 20, 25 01:18 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations -
10 Hard SAT Math Questions (Part - 40)
Dec 18, 25 06:27 PM
10 Hard SAT Math Questions (Part - 40)
