WORD PROBLEMS ON SIMPLE INTEREST

Problem 1 :

Find the simple interest for 2 years on $2000 at 6% per year.

Solution :

Formula for simple interest :

I = Prt

Substitute P = 2000, t = 2 and r = 6% or 0.06.

I = 2000 ⋅ 0.06 ⋅ 2

I = $240

Problem 2 :

In simple interest, a sum of money doubles itself in 10 years. Find the number of years it will take to triple itself.

Solution :

Let P be the sum of money invested.

Given : Sum of money doubles itself in 10 years.

Then, P will become 2P in 10 years.

Now we can calculate interest for ten years as given below

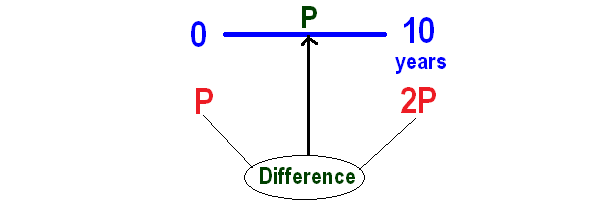
From the above calculation, P is the interest for the first 10 years.

In simple interest, interest earned will be same for every year.

So, interest earned in the next 10 years also will be P.

It has been explained below.

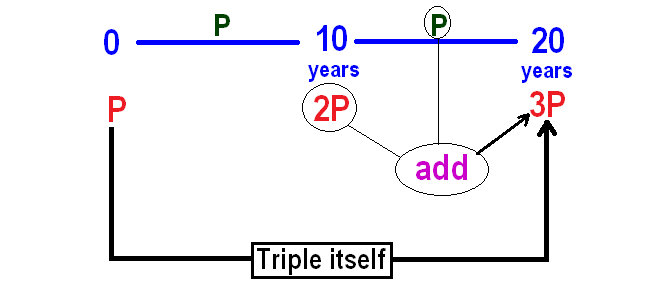
So, it will take 20 years for the principal to become triple itself.

Problem 3 :

In simple interest, a sum of money amounts to $ 6200 in 2 years and $ 7400 in 3 years. Find the principal.

Solution :

At the end of 2 years, we get $6200.

At the end of 3 years, we get $7400.

From these two information, we can get the interest earned in the 3rd year as given below.

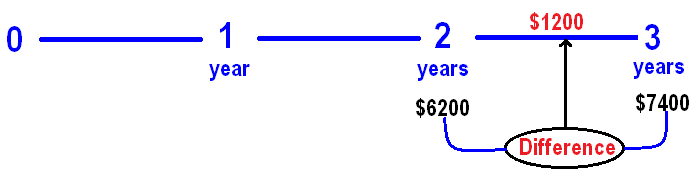
In simple interest, interest will be same for every year.

Based on this, we can calculate the principal as given below

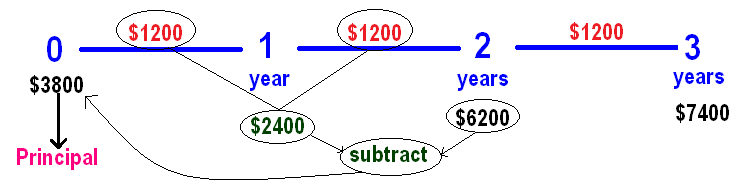
So, the principal is $3800.

Problem 4 :

A sum of $46875 was lent out at simple interest and at the end of 1 year 8 months, the total amount was $50000.Find the rate of interest per year.

Solution :

From the given information, we have

P = 46875 and A = 50000

Interest = Amount - Principal

I = 50000 - 46875

I = 3125

The value of n must always be in years. But in the question, it is given in both years and months.

To convert months to years, divide the given months by 12.

1 year 8 months = 1⁸⁄₁₂ years or 1⅔ years

So, the value of t is 1⅔ or ⁵⁄₃.

Formula for simple interest :

I = Prt

Substitute P = 46875 and t = ⁵⁄₃.

3125 = 46875 ⋅ r ⋅ ⁵⁄₃

3125 = 78125 ⋅ r

Divide both sides by 78125.

0.04 = r

0.04 ⋅ 100% = r

4% = r

Problem 5 :

Find the accumulated value of the deposit $2500 made in simple interest for 3.5 years at 5% rate of interest per year.

Solution :

First let us find the interest earned and then we can find the accumulated value.

I = Prt 

Substitute P = 2500, t = 3.5 and r = 0.05.

I = 2500 ⋅ 0.05 ⋅ 3.5

I = 437.50

Accumulated value :

A = P + I

A = 2500 + 437.50

A = $2937.50

Problem 6 :

How much interest will be earned on $3000 at 7% simple interest per year for 9 months ?

Solution :

Formula for simple interest :

I = Prt ----(1)

Substitute P = 3000 and r = 7%.

The value of n must always be in years. But in the question, it is given in months. 

To convert months to years, divide the given months by 12.

9 months = ⁹⁄₁₂ years or ¾ years

n = ¾

In (1), substitute P = 3000, r = 0.07 and t = ¾.

I = 3000 ⋅ 0.07 ⋅ ¾

I = $157.50

Problem 7 :

What sum of money will produce $28600 as interest in 3 years and 3 months at 2.5% per year simple interest ?

Solution :

Formula for simple interest :

I = Prt ----(1)

The value of n must always be in years. But in the question, it is given in both years and months. 

To convert months to years, divide the given months by 12.

3 years 3 months = 3³⁄₁₂ years or 3¼ years

n = 3¼ or ¹³⁄₄

Substitute I = 28600, r = 0.025 and t = ¹³⁄₄ in (1)

28600 = P ⋅ 0.025 ⋅ ¹³⁄₄

2860000 = P ⋅ 0.025 ⋅ 3.25

2860000 = P ⋅ 8.125

Divide both sides by 8.125.

352000 = P

Required sum of money is $352,000.

Problem 8 :

Mr. Abraham  invested an amount of $13900 divided in two different schemes A and B at the simple interest rate of 14% p.a. and 11% p.a. respectively. If the total amount of simple interest earned in 2 years be $ 3508, what was the amount invested in Scheme B ?

Solution :

Let m be the amount invested in scheme B. 

Then the amount invested in scheme A = 13900 - m.

Interest in scheme (A) + Interest in scheme (B) = 3508 

(13900 - m) ⋅ 0.14 ⋅ 2 + m ⋅ 0.11 ⋅ 2 = 3508

(13900 - m) ⋅ 0.28  +  0.22m = 3508

3892 - 0.28m  +  0.22m = 3508

3892 - 0.06m = 3508

3892 - 3508 = 0.06m

384 = 0.06m

m = 6400 

The amount invested in scheme B is $6,400.

Problem 9 :

Lily took a loan of $1200 with simple interest for as many years as the rate of interest. If she paid $432 as interest at the end of the loan period, what was the rate of interest?

Solution :

Let m be the rate of interest. 

Given : The rate of interest and the number of years are same.

Then, the number of years = m.

Formula for simple interest :

I = Prt 

Substitute I = 432, P = 1200, r = 0.01m and t = m. 

432 = 1200 ⋅ 0.01m ⋅ m

432 = 12m²

Divide both sides by 12.

36 = m²

6² = m²

6 = m

The rate of interest is 6%.

Problem 10 :

A lent $5000 to B for 2 years and $3000 to C for 4 years on simple interest at the same rate of interest and received $2200 in all from both of them as interest. Find the rate of interest per year.

Solution :

Let m be the rate of interest.

Interest from B + Interest from C = 2200

5000 ⋅ 0.01m ⋅ 2  + 3000 ⋅ 0.01m ⋅ 4 = 2200

100m  + 120m = 2200

220m = 2200

Divide both sides by 220.

m = 10

The rate of interest is 10%.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.