WORD PROBLEMS ON RATIO AND PROPORTION

Problem 1 :

The average age of three boys is 25 years and their ages are in the proportion 3 : 5 : 7. Find the age of the youngest boy.

Solution :

From the ratio 3 : 5 : 7, the ages of three boys are 3x, 5x and 7x.

Average age of three boys = 25

(3x + 5x + 7x)/3 = 25

15x = 75

x = 5

Age of the first boy = 3x

= 3(5)

= 15

Age of the first boy = 5x

= 5(5)

= 25

Age of the first boy = 7x

= 7(5)

= 105

So, the age of the youngest boy is 15 years.

Problem 2 :

John weighs 56.7 kilograms. If he is going to reduce his weight in the ratio 7 : 6, find his new weight.

Solution :

Given : Original weight of John = 56.7 kg.

He is going to reduce his weight in the ratio 7:6.

We can use the following hint to find his new weight, after it is reduced in the ratio 7 : 6.

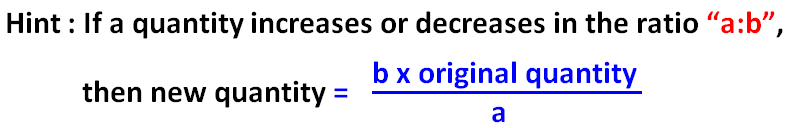
His new weight is

= (6 ⋅ 56.7)/7

= 48.6 kg.

So, John's new weight is 48.6 kg.

Problem 3 :

The ratio of the no. of boys to the no. of girls in a school of 720 students is 3 : 5. If 18 new girls are admitted in the school, find how many new boys may be admitted so that the ratio of the no. of boys to the no. of girls may change to 2 : 3.

Solution :

Sum of the terms in the given ratio is

= 3 + 5

= 8

So, no. of boys in the school is

= 720 ⋅ (3/8)

= 270 

No. of girls in the school is

= 720 ⋅ (5/8) 

= 450

Given : Number of new girls admitted in the school is 18.

Let x be the no. of new boys admitted in the school.

After the above new admissions,

No. of boys in the school = 270 + x

No. of girls in the school = 450 + 18 = 468

Given : The ratio after the new admission is 2 : 3.

Then, we have

(270 + x) : 468 = 2 : 3

Use cross product rule.

3(270 + x) = 468 ⋅ 2

810 + 3x = 936

3x = 126

x = 42

So, the number of new boys admitted in the school is 42.

Problem 4 :

The monthly incomes of two persons are in the ratio 4 : 5 and their monthly expenditures are in the ratio 7 : 9. If each saves $50 per month, find the monthly income of the second person.

Solution :

From the given ratio of incomes ( 4 : 5 ),

Income of the 1st person = 4x

Income of the 2nd person = 5x

(Expenditure  =  Income - Savings)

Then, expenditure of the 1st person = 4x - 50

Expenditure of the 2nd person = 5x - 50

Expenditure ratio = 7 : 9 (given)

So, we have

(4x - 50) : (5x - 50) = 7 : 9

Use cross product rule.

9(4x - 50) = 7(5x - 50)

36x - 450 = 35x - 350

x = 100

Then, the income of the second person is

= 5x

= 5(100)

= 500

So, income of the second person is $500.

Problem 5 :

The ratio of the prices of two houses was 16 : 23. Two years later when the price of the first has increased by 10% and that of the second by $477, the ratio of the prices becomes 11 : 20. Find the original price of the first house.

Solution :

From the given ratio 16 : 23,

Original price of the 1st house = 16x

Original price of the 2nd house = 23x

After increment in prices,

Price of the 1st house = 16x + 10% of 16x 

= 16x + 1.6x

= 17.6x

Price of the 2nd house = 23x + 477

After increment in prices, the ratio of prices becomes 11:20.

17.6x : (23x + 477) = 11 : 20

Use cross product rule.

20(17.6x) = 11(23x + 477)

352x = 253x + 5247

99x = 5247

x = 53

Then, original price of the first house is

= 16x

= 16(53)

= 848

So, original price of the first house is $848.

Problem 6 :

Two numbers are respectively 20% and 50% are more than a third number, Find the ratio of the two numbers.

Solution :

Let x be the third number.

Then, the first number is

= (100 + 20)% of x

= 120% of x

= 1.2x

The second number is

= (100 + 50)% of x

= 150% of x

= 1.5x

The ratio between the first number and second number is

= 1.2x : 1.5x

= 1.2 : 1.5

= 12 : 15

= 4 : 5

So, the ratio of two numbers is 4 : 5.

Problem 7 :

The milk and water in two vessels A and B are in the ratio 4:3 and 2:3 respectively. In what ratio, the liquids in both the vessels be mixed to obtain a new mixture in vessel C consisting half milk and half water ?    

Solution :

Vessel A :

[4 : 3 ----> 4 + 3 = 7, M ----> 4/7, W ----> 3/7]

Let x be the quantity of mixture taken from vessel A to obtain a new mixture in vessel C.

Quantity of milk in x = (4/7)x = 4x/7

Quantity of water in x = (3/7)x = 3x/7

Vessel B :

[2 : 3 ----> 2 + 3 = 5, M ---> 2/5, W ----> 3/5]

Let y be the quantity of mixture taken from vessel B to obtain a new mixture in vessel C.

Quantity of milk in y = (2/5)y = 2y/5

Quantity of water in y = (3/5)y = 3y/5

Vessel A and B :

Quantity of milk from A and B is

= 4x/7 + 2y/5

= (20x + 14y)/35

Quantity of water from A and B is

= (3x/7) + (3y/5)

= (15x + 21y)/35

According to the question, vessel C must consist half of the milk and half of the water.

That is, in vessel C, quantity of milk and water must be same.

There fore,

quantity of milk in (A + B) = quantity of water in (A + B)

(20x + 14y)/35 = (15x + 21y)/35

20x + 14y = 15x + 21y

5x = 7y

x/y = 7/5

x : y = 7 : 5

So, the required ratio is 7 : 5.

Problem 8 :

A vessel contains 20 liters of a mixture of milk and water in the ratio 3:2. From the vessel, 10 liters of the mixture is removed  and replaced with an equal quantity of pure milk. Find the ratio of milk and water in the final mixture obtained.    

Solution :

[3 : 2 ----> 3 + 2 = 5, M ----> 3/5, W ----> 2/5]

In 20 liters of mixture,

no. of liters of milk = 20 ⋅ 3/5 = 12

no. of liters of water = 20 ⋅ 2/5 = 8

Now, 10 liters of mixture removed.

In this 10 liters of mixture, milk and water will be in the ratio 3 : 2.

no. of liters of milk in this 10 liters = 10 ⋅ 3/5 = 6

no. of liters of water in this 10 liters = 10 ⋅ 2/5 = 4

After removing 10 liters (1st time),

no. of liters of milk in the vessel = 12 - 6 = 6

no. of liters of water in the vessel = 8 - 4 = 4

Now,  we add 10 liters of pure milk in the vessel,

After adding 10 liters of pure milk in the vessel,

no. of liters of milk in the vessel = 6 + 10 = 16

no. of liters of water in the vessel = 4 + 0 = 4

After removing 10 liters of mixture and adding 10 liters of pure milk, the ratio of milk and water is

= 16 : 4

= 4 : 1

So, the required ratio is 4 : 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.