WORD PROBLEMS ON RATE OF CHANGE

Problem 1 :

A conical water tank with vertex down of 12 meters height has a radius of 5 meters at the top. If water flows into the tank at a rate 10 cubic m/min, how fast is the depth of the water increases when the water is 8 meters deep ?

Solution :

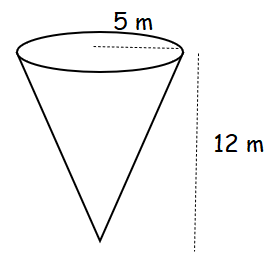
Let r and h be radius and height of the cone respectively,

r/h  =  5/12

r  =  5h/12

Volume of tank(V)  =  (1/3)πr²h

V  =  (1/3)π(5h/12)²h

V  =  (25/432)πh³

dV/dt  =  (25/432)π(3h²dh/dt)

dV/dt  =  10 cubic m/min, h  =  8

10  =  (25/432)π(3)(64) dh/dt

dh/dt  =  9π/10 meter/minute

Problem 2 :

A ladder 17 meter long is leaning against the wall. The base of the ladder is pulled away from the wall at a rate of 5 m/s. When the base of the ladder is 8 meters from the wall.

(i) How fast is the top of the ladder moving down the wall?

(ii) At what rate, the area of the triangle formed by the ladder, wall, and the floor, is changing?

Solution :

Let x be the distance from the wall to the foot of the ladder.

y be the distance of the top of the ladder from the ground.

Given :

dx/dt  =  5 m/s, dy/dt  =  ? when x  =  8

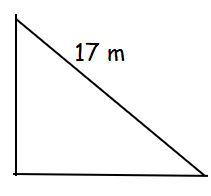
x² + y²  =  17²  ----(1)

8² + y²  =  17²

64 + y²  =  289

y²  =  289-64

y²  =  225

y  =  15

Differentiating (1)

2x(dx/dt) + 2y(dy/dt)  =  0

2(8)(5) + 2(15)(dy/dt)  =  0

30(dy/dt)  =  -80

dy/dt  =  -8/3

(ii)  Area of the triangle  =  (1/2) x base x height

A  =  (1/2) [xy]

dA/dt  =  (1/2) [x(dy/dt) + y(dx/dt)]

dA/dt  =  (1/2) [8(-8/3) + 15(5)]

dA/dt  =  (1/2) [(-64/3) + 75]

dA/dt  =  -26.83

Problem 3 :

A police jeep, approaching an orthogonal intersection from the northern direction, is chasing a speeding car that has turned and moving straight east. When the jeep is 0.6 km north of the intersection and the car is 0.8 km to the east. The police determine with a radar that the distance between them and the car is increasing at 20 km/hr. If the jeep is moving at 60 km/hr at the instant of measurement, what is the speed of the car?

Solution :

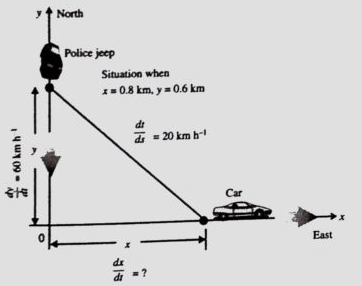
x² + y²  =  s²  ---(1)

(0.8)² + (0.6)²  =  s²

0.64 + 0.36  =  s²

s  =  1

Differentiating (1) with respect to t

2x(dx/dt) + 2y(dy/dt)  =  2s(ds/dt)

(0.8)(dx/dt) + (0.6)(-60)  =  1(20)

(0.8)(dx/dt) -36  =  20

(0.8)(dx/dt)  =  56

dx/dt  =  56/0.8

dx/dt  =  70 km/hr

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.