WORD PROBLEMS ON PROPORTIONS WORKSHEET

Problem 1 :

Look at the picture below.

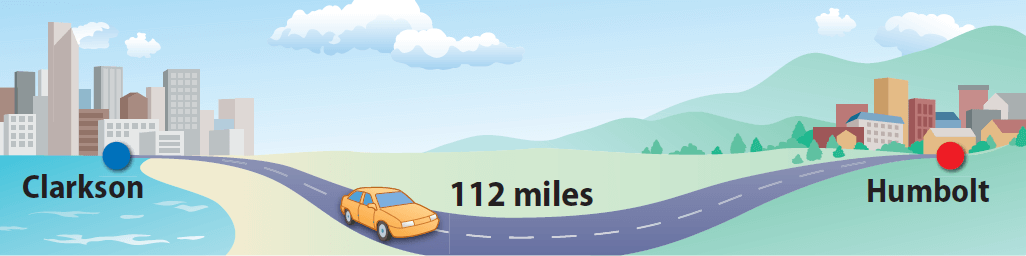
Janet drives from Clarkson to Humbolt in 2 hours. Suppose If she maintains the same driving rate, how many miles can she drive in 10 hours?

Problem 2 :

The distance Ali runs in 40 minutes is 3 miles. At this rate, how far can he run in 60 minutes?

Problem 3 :

In 15 minutes, Lena can finish 2 math problems. At that rate, how many math problems can she finish in 75 minutes ? Use a double number line to find the answer.

Problem 4 :

Ms. Reynolds has a system of 10 sprinklers that water her entire lawn. The sprinklers run one at a time, and each runs for the same amount of time. The first 4 sprinklers run for a total of 50 minutes. How long does it take to water her entire lawn?

Problem 5 :

A disaster relief team consists of engineers and doctors in the ratio of 2 : 5.

a) If there are 18 engineers, find the number of doctors.

b) If there are 65 doctors, find the number of engineers.

Problem 6 :

The ratio of two angles in a triangle is 3 : 1.

Find the :

a) larger angle if the smaller is 18°

b) smaller angle if the larger is 63°

Problem 7 :

The ratio of teachers to students in a school is 1 : 15. If there are 675 students, how many teachers are there?

Problem 8 :

An MP3 player is bought for $240 and sold for $270. Find the ratio of the cost price to the selling price.

Problem 9 :

The maximum speeds of a boat and a car are in the ratio 2 : 7. If the maximum speed of the boat is 30 km per hour, find the maximum speed of the car.

Problem 10 :

A farmer has sheep and cattle in the ratio 8 : 3.

a)  How many sheep has the farmer if he has 180 cattle?

b)  Find the ratio of the number of sheep to the total number of animals.

c)  Find the ratio of the total number of animals to the number of cattle.

Answers

1. Answer :

Given : Janet drives from Clarkson to Humbolt in 2 hours.

From the above information, we can get the following ratio between time and distance.

2 : 112 -----> (1)

Let A be the number of miles that she can drive in 10 hours.

Then, we have

10 : A ----> (2)

Since she maintains the same driving rate, the ratios (1) and (2) are equivalent.

So, we get the proportion

2 : 112 = 10 : A

Let us apply cross product rule

2A = 112 x 10

A = ⁽¹¹² ˣ ¹⁰⁾⁄₂

A = 560

So, she can drive 560 miles in 10 hours.

2. Answer :

Let A be the number of miles that he can run in 60 minutes.

From the given information, we can write the following proportion.

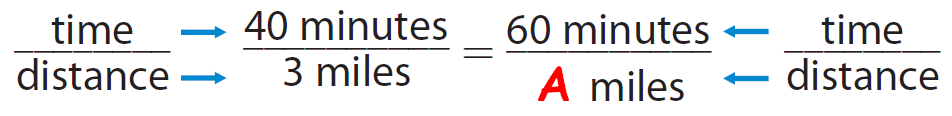
In the proportion

40 : 3 = 60 : A

the extremes are 40 & A and means are 3 & 60.

Let us apply cross product rule.

40A = 3 x 60

Dividing by 40 on both sides, we get

A = ¹⁸⁰⁄₄₀

A = ⁹⁄₂ 

A = 4½

At this rate, Ali can run 4½ miles in 60 minutes.

3. Answer :

Given : Lena can finish 2 math problems in 15 minutes.

From the above information, we can get the following ratio between math problems and minutes.

2 : 15 -----> (1)

Let "B" be the number of math problems that she can finish in 75 minutes.

Then, we have

B : 75 -----> (2)

Since she maintains the same rate, the ratios (1) and (2) are equivalent.

So, we get the proportion

2 : 15 = B : 75

Let us apply cross product rule

2 x 75 = 15B

⁽² ˣ ⁷⁵⁾⁄₁₅ = B

10 = B

So, Lena can finish 10 math problems in 75 minutes.

4. Answer :

Let T be the time takes to water the entire lawn.

From the given information, we can write the following proportion.

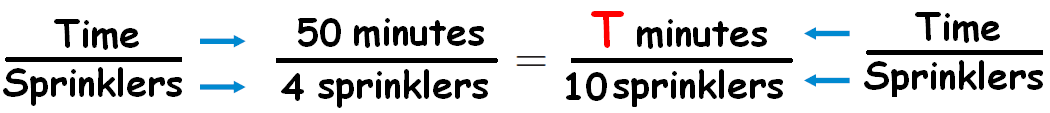
In the proportion

50 : 4 = T : 10

the extremes are 50 & 10 and means are 4 & T.

Let us apply cross product rule.

50 x 10 = 4T

500 4T

Divide both sides by 4.

125 = T

So, it takes 125 minutes or 2 hours 5 minutes to water her entire lawn.

5. Answer :

(a)  Let x be the number of doctors in the team.

According to the information, the number of engineers and doctors are in the ratio 2 : 5.

2 : 5 = 18 : x

Product of extremes = Product of means

2x = 5 x 18

x = ⁽⁵ ˣ ¹⁸⁾⁄₂

x = 45

So, the number of doctors in that team is 45.

b) Let y be the number of engineers in that team.

2 : 5 = y : 65

2 x 65 = 5y

⁽² ˣ ⁶⁵⁾⁄₅ = y

26 = y

So, the number of engineers in that team is 26.

If there are 65 doctors, find the number of engineers.

6. Answer :

The ratio of two angles in a triangle is 3 : 1.

From the given ratio, 

larger angle = 3x

smaller angle = x

(a) Finding larger angle, if the smaller is 18°.

3x = 3 x 18

= 54

If smaller angle is 18°, then the larger angle is 54°.

b) Finding smaller angle, if the larger is 63°.

3x = 63

x = 21

If larger angle is 63°, then the smaller angle is 21°.

7. Answer :

Ratio of teachers to students = 1 : 15.

Number of teachers = x and students = 15x

Total number of students = 675.

15x = 675

x = 45

So, number of teachers is 45.

8. Answer :

Cost price of MP3 = $240 and selling price = $270.

costot price : selling price = 240 : 270

= ²⁴⁰⁄₂₇₀

= ⁸⁄₉

= 8 : 9

So, the cost price and selling price are in the ratio 8 : 9.

9. Answer :

Ratio of speeds of boat and car = 2 : 7.

2x = Speed of Boat and 7x = Speed of car

Speed of boat = 30 km per hour

2x = 30

x = 15

Speed of car = 7(15)

= 105 km/hr

10. Answer :

8x = Number of sheep and 3x = number of cattle

(a) Number of cattle = 180

3x = 180

x = 60

Number of sheep = 8(60) = 480.

b) Total number of animal = 3x + 8x.

= 11x

= 11(60)

= 660

Number of sheep : Number of animal

= 480 : 660

= ⁴⁸⁰⁄₆₆₀

= 8 : 11

c) Total number of cattle = 660.

660 : 180

By simplifying, we get

= 66 : 18

= 11 : 3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.