WORD PROBLEMS INVOLVING RIGHT TRIANGLE

Example 1 :

The size of a computer monitor is the length across its diagonal. If a computer monitor is 34.4 cm long and 27.5 cm high, what size is it?

Solution :

In figure, given

Height of a computer monitor (a)  =  27.5 cm

Length of base (b)  =  34.4 cm 

Let c be the length of diagonal.

By using Pythagoras theorem,

a² + b²  =  c²

(27.5)² + (34.4)²  =  c²

 c²  =  756.25 + 1183.36 

c²  =  1939.61

c  =  √1939.61

c  =  44.0 cm

So, length of the diagonal c is 44.0 cm.

Example 2 :

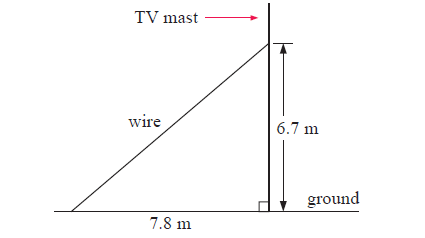
(a)  Find the length of the wire shown supporting the TV mast. 

(b) There are six wires which support the mast.

i)  Find their total length.

ii)  If 3% extra wire is needed for tying, how many meters of wire need to be purchased?

Solution :

(a) By finding length of hypotenuse, we can find the length of wire needed.

In figure, 

a  =  6.7 m and b  =  7.8 m

To find the length of the wire c  =  ?

By using Pythagoras theorem,

(6.7)² + (7.8)²  =  c²

44.89 + 60.84  =  c²

105.73  =  c²

c  =  √105.73

c  =  10.28 m

So, length of the wire c is 10.28 m.

(b)

(i)  Length of the one wire is 10.28 m.

Length of 6 wires  =  10.28 × 6

=  61.68 m

So, total length is 61.7 m

(ii) If 3% extra wire is needed for tying, how many meters of wire need to be purchased? The wire must be purchased in a whole number of meters.

We have already 6 wires.

We need 3% extra wire,

=  6 + 3% of 61.68

=  6.18

So, total wires 6.18

Total meters of wires purchased 

=  Length of the wire × total wires

=  10.28 × 6.18

=  63.53 m

So, 64 m of wire to be purchased.

Example 3 :

Metal supports are made as shown. They are fitted from the lower edge of the table top to the legs. The flat ends of the supports are 2 cm long. Find the length of the metal needed to make the 8 supports used to stabilise the table.

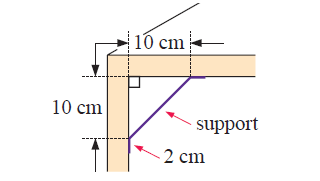
In figure, given

We see this right triangle,

Top metal fits a  =  10 cm

Lower edge metal fits b  =  10 cm

Length of the metal support c  =  ?

By using Pythagoras theorem,

a² + b²  =  c²

10² + 10²  =  c²

100 + 100  =  c²

200  =  c²

c  =  √200

c  =  14.14 cm

Length of the metal supports c  =  14.14 cm

Length of the metal supports 2 cm long top and lower,

So, Length of the metal supports  =  18.14 cm

We need,

Length of the metal 8 supports  =  18.14 × 8

=  145.12 cm

Therefore, Length of the metal 8 supports is  145.12 cm.

Example 4 :

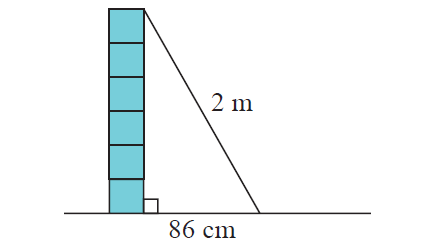
A ladder is 2 meters long. It leans against a wall so the base is 86 cm from the wall. 

a) Write 86 cm in meters. 

b) How far up the wall does the ladder reach?

Solution :

(a)  86 cm  =  0.86 m

(b)  Using Pythagorean theorem, we get

Let x be the distance reached by the ladder.

(0.86)² + x²  =  2²

0.7396 + x²  =  4

x²  =  4-0.7396

x²  =  3.2604

x  =  1.80

Example 5 :

Heidi has made a rectangular cushion cover which measures 36 cm long by 32 cm wide. She wants to put lace across one diagonal on each side. 

a) Find the length of the diagonal. 

b) Find the total length of lace required, if 4 cm extra is allowed for finishing off the ends.

c) Calculate the cost of the lace at $2.30 per meter

Solution :

(a)  Let x be the length of diagonal.

Using Pythagorean theorem, 

36² + 32²  =  x²

1296 + 1024  =  x²

 x²  =  2320

x  =  48.16 

x  =  48.2 m

(b)  Total length of lace  =  48.2(2)

=  96.4

4 m is needed, then length of lace  =  96.4+4

=  100.4

(c)  Required cost  =  100.4(2.30)

=  $231

Example 6 :

A square garden with sides 100 m is divided into two triangular plots by a fence along one diagonal.

a) What is the length of the fence in meters (to 1 decimal place) ?

b) If the fence costs $15.50 per meter, what is the total cost ?

Solution :

Let x be the length of diagonal.

x²  =  100²+100²

x²  =  10000+10000

x²  =  20000

x  =  141.4 m

(b)  Cost of fencing  =  $5.50 per meter

Required cost  =  141.4(5.50)

=  $777.7

Example 7 :

A 160 m long water pipe runs along the diagonal of a square paddock. What are the lengths of the sides of the paddock?

Solution :

Length of diagonal pipe  =  160 m

Let x be the side length square paddock.

x²+x²  =  160²

2x²  =  25600

x  =  113.14 m

So, side length of paddock is 113.14 m

Example 8 :

A garden gate is 1.2 meters wide and 1.2 meters high. The gate is strengthened by a diagonal strut.

a) How long is the strut?

b) Calculate the length of steel needed for the frame of the gate, including the strut.

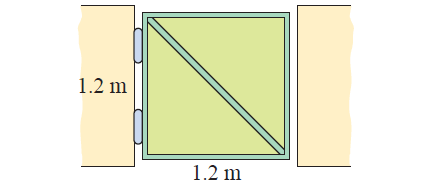
Solution :

(a)  Let x be the length of diagonal.

x²  =  (1.2)² + (1.2)²

x²  =  1.44+1.44

x²  =  2.88

x  =  1.7 m

(b)  Length of steel needed including the diagonal

=  4(1.2) + 1.7

=  4.8+1.7

=  6.5 m

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.