WHAT IS LEAST COMMON MULTIPLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Least common multiple is the smallest number which is a multiple of the given numbers.
For example, consider the numbers 2 and 3.
Now, list out the whole numbers which are multiples of both both 2 and 3.
6, 12, 18, 24, ..........
All the above numbers are multiples of both 2 and 3.
Is there any whole number less than 6 which is a multiple of both 2 and 3?
The answer is NO.
So, 6 is the smallest whole number which is a multiple of both 2 and 3.
In other words, 6 is the smallest whole number which is evenly divisible by both 2 and 3.
Therefore, 6 is the least common multiple of 2 and 3.
More Examples :
Least common multiple of 4 and 6 = 12
Least common multiple of 10 and 15 = 30
Least common multiple of 5 and 10 = 10
The above examples of finding least common multiple of two whole numbers are pretty easy. Incase, we have bogger numbers or more than two numbers, how to find the least common multiple?
We can find the least common multiple of two or more numbers by the following methods.
1. Division Method
2. Prime factorization Method
(LCM ----> Least Common Multiple)
Example :
Find the LCM of 156 and 124.
Solution by Division Method :
Step 1 :
Start with the smallest prime factor and go on dividing till all the numbers are divided as shown below.
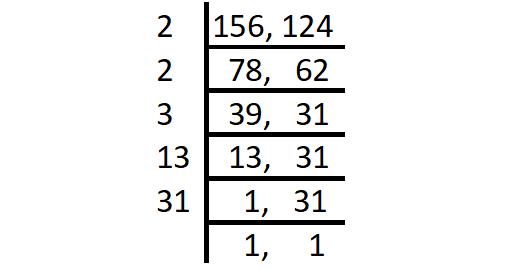
Step 2 :
LCM = Product of all prime factors
= 2 x 2 x 3 x 13 x 31
= 4836
Thus, the LCM of 156 and 124 is 4836.
Solution by Prime Factorization Method :
Step 1 :
Write the prime factors of 156 and 124 as shown below (use of divisibility test rules will also help).
156 = 2 x 2 x 3 x 13
124 = 2 x 2 x 31
Step 2 :
The prime factor 2 appears a maximum of 2 times in the prime factorization of 156 and 124.
The prime factors 3 and 13 appear only 1 time in the prime factorization of 156, the prime factor 31 appears only 1 time in the prime factorization of 124.
Hence, the required LCM is
= (2 x 2) x 3 x 13 x 31
= 4836
Solved Problems
Problem 1 :
Find the LCM of the following set of numbers using prime factorization method.
6, 9
Solution :
Step 1 :
Write the prime factors of 6 and 9 as shown below.
6 = 2 x 3
9 = 3 x 3
Step 2 :
The prime factor 3 appears a maximum of 2 times in the prime factorization of 9.
The prime factor 2 appears only 1 time in the prime factorization of 6.
Hence, the required LCM is
= (3 x 3) x 2
= 9 x 2
= 18
Problem 2 :
Find the LCM of the following set of numbers using prime factorization method.
8, 12
Solution :
Step 1 :
Write the prime factors of 8 and 12 as shown below.
8 = 2 x 2 x 2
12 = 2 x 2 x 3
Step 2 :
The prime factor 2 appears a maximum of 3 times in the prime factorization of 8.
The prime factor 3 appears only 1 time in the prime factorization of 12.
Hence, the required LCM is
= (2 x 2 x 2) x 3
= 8 x 3
= 24
Problem 3 :
Find the LCM of the following set of numbers using division method.
16, 24
Solution :
Step 1 :
Start with the smallest prime factor and go on dividing till all the numbers are divided as shown below.
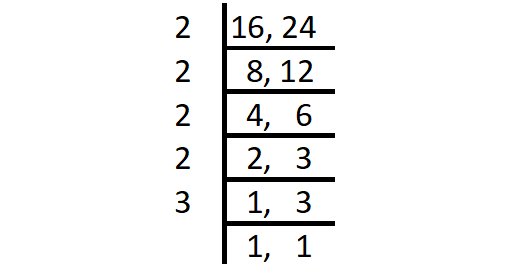
Step 2 :
LCM = Product of all prime factors
= 2 x 2 x 2 x 2 x 3
= 48
Thus, the LCM of 16 and 24 is 48.
Problem 4 :
Find the LCM of the following set of numbers using division method.
64, 80
Solution :
Step 1 :
Start with the smallest prime factor and go on dividing till all the numbers are divided as shown below.
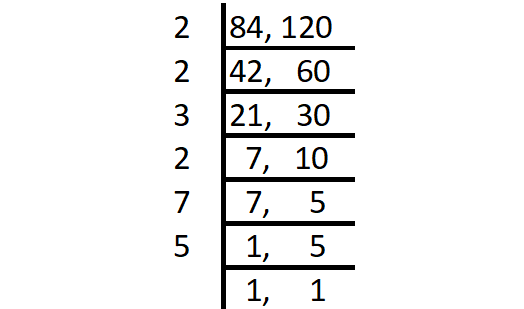
Step 2 :
LCM = Product of all prime factors
= 2 x 2 x 3 x 2 x 7 x 5
= 840
Thus, the LCM of 64 and 80 is 840.
Problem 5 :
Find the LCM of the following set of numbers using prime factorization method.
8, 12, 16
Solution :
Step 1 :
Write the prime factors of 8, 12 and 16 as shown below.
8 = 2 x 2 x 2
12 = 2 x 2 x 3
16 = 2 x 2 x 2 x 2
Step 2 :
The prime factor 2 appears a maximum of 4 times in the prime factorization of 16.
The prime factor 3 appears only 1 time in the prime factorization of 12.
Apart from 2 and 3, we don't find any other prime factors.
Hence, the required LCM is
= (2 x 2 x 2 x 2) x 3
= 16 x 3
= 48
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
GMAT Quantitative Reasoning Questions and Answers
Dec 27, 25 09:33 PM
GMAT Quantitative Reasoning Questions and Answers -
10 Hard SAT Math Questions (Part - 40)
Dec 25, 25 08:30 AM
10 Hard SAT Math Questions (Part - 40) -
10 Hard SAT Math Questions (Part - 41)
Dec 24, 25 07:58 PM
10 Hard SAT Math Questions (Part - 41)

