VOLUME

To find volume of any 3-D shape, you have to multiply the base area and height. Based on this, we can find the area of 3-D shapes like cylinder, cone, sphere etc. 

Cylinder

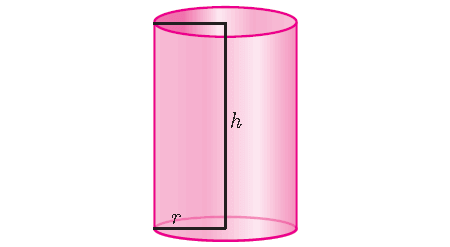
Let the area of the base of a cylinder be B and the height of the cylinder be h. Write a formula for the cylinder’s volume V.

V = Bh

The base of a cylinder is a circle, so for a cylinder,

B = πr²

Then, we have

V = πr²h cubic units

Cone

Consider a right circular cylinder and three right circular cones of same base radius and height as that of the cylinder.

The contents of three cones will exactly occupy the cylinder.

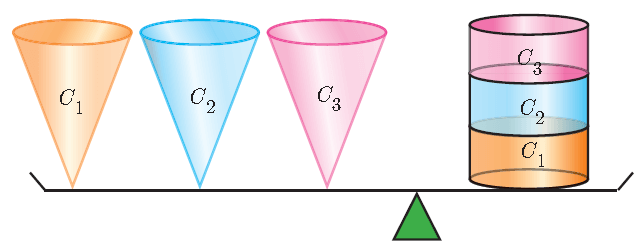
Then,

When we model the volume of a sphere, we will be getting the following result. 

3 x (Volume of a cone) = Volume of cylinder

3 x (Volume of a cone) = πr²h

Volume of the cone = 1/3 · πr²h cubic units

Sphere

Consider a sphere and two right circular cones of same base radius and height such that twice the radius of the sphere is equal to the height of the cones.

Then we can observe that the contents of two cones will exactly occupy the sphere.

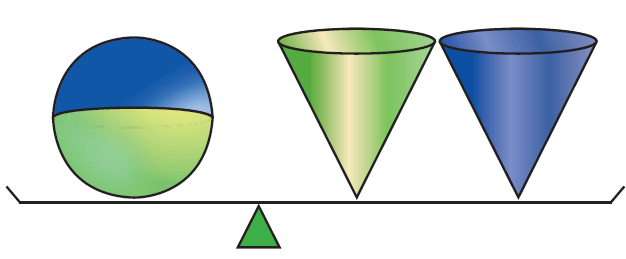
Then, 

Volume of sphere = 2 x (Volume of a cone)

Volume of a sphere = 2 x (1/3 · πr²h)

Volume of a sphere = 2/3 · πr²h

A sphere always has a height which is equal to twice the radius.

So, substitute 2r for h.

Volume of sphere = 2/3 · πr²(2r)

Simplify.

Volume of sphere = 4/3 · πr³ cubic units

Prism

Prism is basically a 3D shape. Even though we have different formulas to find volume of different kinds of prisms, the basic idea of finding volume is to multiply the base area and height of the prism.

When we are trying to find volume of a prism, we have to consider the following cases. 

Case 1 : 

Let the base of a prism be a rectangle or square. If all the side walls are either rectangles or squares (that is, no side wall is triangle), then prism will look like as given below. 

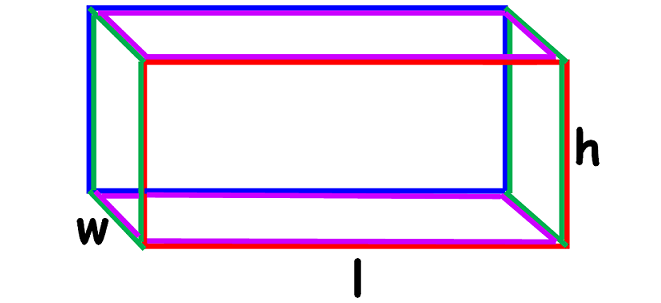
The formula to find volume of the above prism 

=  Base area x Height

Case 2 :

Let the base of a prism be a rectangle or square. If two of the side walls side walls are triangles and other two side walls are rectangles or squares, then prism will look like as given below. 

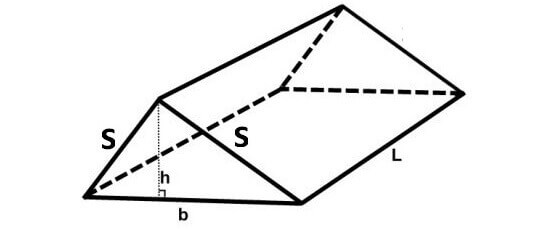
The formula to find volume of the above prism 

=  (1/2) x Base area x Height

Case 3 :

Let the base of a prism be a triangle. If all of the side walls are rectangles or squares, then the prism will look like as given below.  

The formula to find volume of the above prism 

=  Base area x Height

Case 4 : 

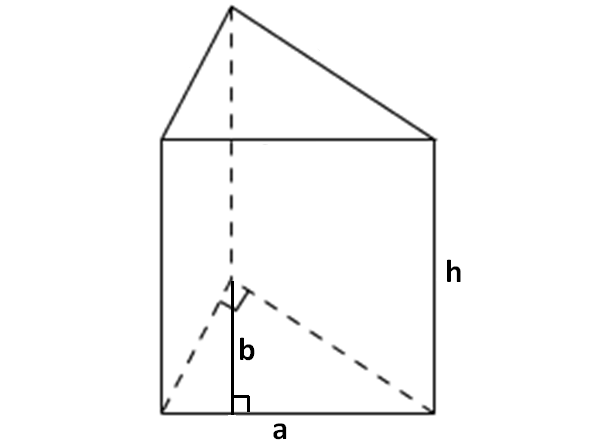
Let the base of a prism be a rectangle or square or triangle. If all of the side walls are triangles, then the prism will be a pyramid and it will look like as given below. 

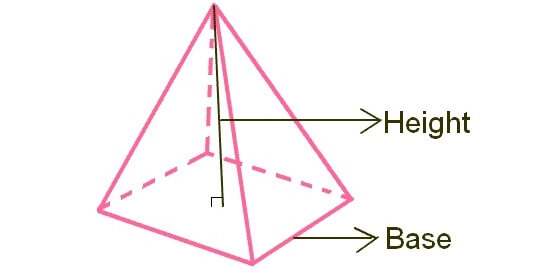
The formula to find volume of the above pyramid 

= (1/3) x Base Area x Height

Problem 1 :

A movie theater designs two bags to hold 96 cubic inches of popcorn.

(a) Find the height of each bag.

(b) Which bag should the theater choose to reduce the amount of paper needed? Explain.

Solution :

Bag A :

Length = 4 inches, width = 3 inches and height = h

Quantity of popcorn in bag A = 96 cubic inches

length x width x height = 96

4 x 3 x h = 96

12 x h = 96

h = 96/12

h = 8 inches

So, the height of the popcorn bag A is 8 inches.

Bag B :

Length = 4 inches, width = 4 inches and height = h

Quantity of popcorn in bag A = 96 cubic inches

length x width x height = 96

4 x 4 x h = 96

16 x h = 96

h = 96/16

h = 6 inches

So, the height of the popcorn bag B is 6 inches.

Problem 2 :

Describe and correct the error in finding the volume of the triangular prism.

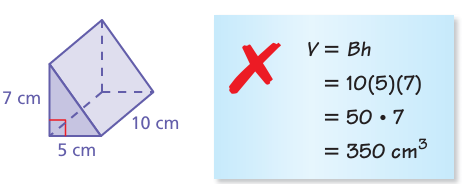
Solution :

Volume of the prism = arae of base x height

Area of base = (1/2) x base x height

base of triangle = 5 cm, height of triangle = 7 cm and height of prism = 10 cm

= (1/2) x 5 x 7 x 10

= 5 x 7 x 5

= 175 cubic inches

The error is :

When we find base area, they didnt use the formula correctly.

Problem 3 :

Each locker is shaped like a rectangular prism. Which has more storage space?

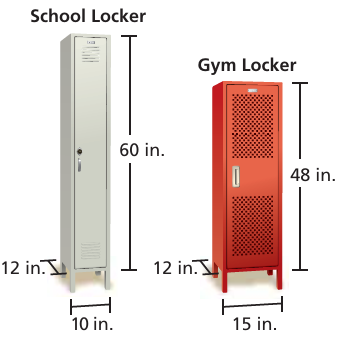
Solution :

Capacity of school locker = length x width x height

= 12 x 10 x 60

= 7200 cubic inches

Capacity of gym locker = length x width x height

= 12 x 15 x 48

= 8640 cubic inches

Problem 4 :

A cereal box is 9 inches by 2.5 inches by 10 inches. What is the volume of the box?

Solution :

Volume of box = length x width x height

= 9 x 2.5 x 10

= 225 cubic inches.

Problem 5 :

Cherise is setting up her tent. Her tent is in the shape of a trapezoidal prism. How many cubic feet of space are in her tent?

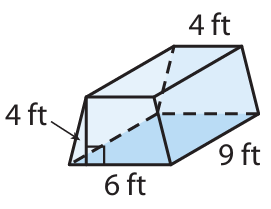
Solution :

Volume of trapezoidal prism = base area x height

base area = (1/2) x h (a + b)

Measures of trapezoidal prism :

parallel sides, a = 6 ft and b = 4 ft and height = 4 ft

height of prsim = 9 ft

Volume = (1/2) x 4 x (4 + 6) x 9

= 2 x 10 x 9

= 180 ft³

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.