VOLUME WITH FRACTIONAL EDGE LENGTHS

In this section, you will learn, how to find volume of a cube or cuboid with fractional edge lengths. 

Fractional Edge Length :

Fractional edge length is the length of each edge of the cube or cuboid is a fraction.

Volume of a Cuboid - Formula

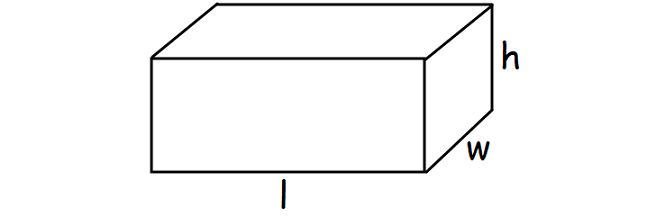
The formula to find volume of the above cuboid is

= Base Area ⋅ Height

= l ⋅ w ⋅ h

Volume of a Cube - Formula

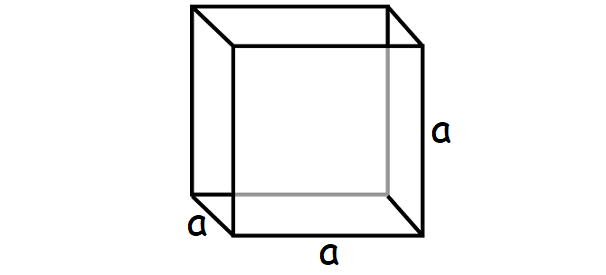
The formula to find volume of the above cube is

= Base Area ⋅ Height

= a ⋅ a ⋅ a

= a³

Example 1 :

Find the volume of the cube given below.

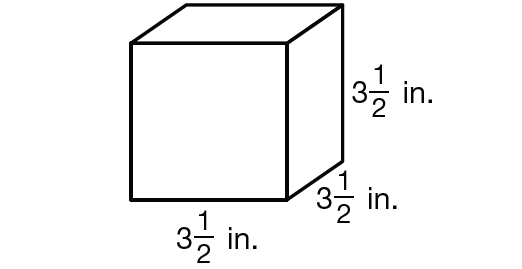
Solution :

Volume of the cube = a³

Substitute a = 3 1/2.

= (3 1/2)³

= (7/2)³

= (7/2) ⋅ (7/2) ⋅ (7/2)

= 343/8

= 42 7/8 cubic inches

Example 2 :

Find the volume of the cuboid given below.

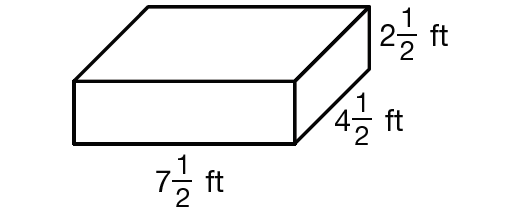
Solution :

Volume of the cuboid = l ⋅ w ⋅ h

Substitute, l = 7 1/2, w = 4 1/2 and h = 2 1/2.

= (7 1/2) ⋅ (4 1/2) ⋅ (2 1/2)

= (15/2) ⋅ (9/2) ⋅ (5/2)

= 675/8

= 84 3/8 cubic ft.

Example 3 :

Find the volume of the cuboid given below.

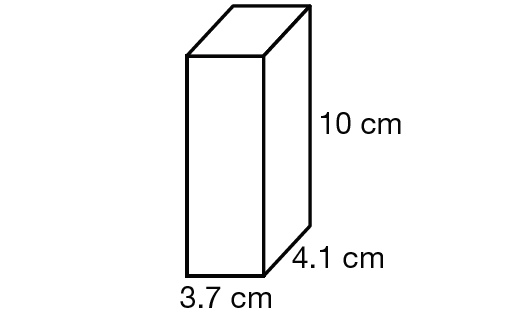
Solution :

Volume of the cuboid = l ⋅ w ⋅ h

Substitute, l = 3.7, w = 4.1 and h = 10.  

= 3.7 ⋅ 4.1 ⋅ 10

= 151.7 cubic cm

Example 4 :

You are baking a cake. The recipe calls for a cake pan that is 9 inches by 11 inches by 2 inches. You have a cake pan that is 10 inches by 10 inches by 2 inches.

a. What is the volume of the recipe’s cake pan?

b. What is the volume of your cake pan?

Solution :

a) Volume of recipie's cake pan = 9 x 11 x 2

= 198 cubic inches

b) Volume of your cake pan = 10 x 10 x 2

= 200 cubic inches

Example 5 :

An office cubicle measures seven feet by eight feet with a five-foot wall. What is the volume of the cubicle?

Solution :

Volume of cubicle = 7 x 8 x 5

= 280 cubic feet

Example 6 :

A cube with side length 4 centimeters is 25% full of sand. What is the volume of the sand?

Solution :

Volume of cube = 4 x 4 x 4

= 64 cm³

Quantity of sand = 25% of 64

= 0.25(64)

= 16 cm³

So, volume of sand is 16 cm^3.

Example 7 :

A cube has sides of length 2 meters. Explain what happens to the volume of the cube if the length of the sides is doubled.

Solution :

Side length of cube = 2 m

When doubling the side length, ne side length = 4 m

Volume of new cube = 4³

= 64 m³

Example 8 :

The area of the shaded face is 72 square inches. What is the volume of the rectangular prism?

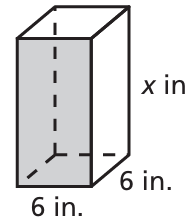
Solution :

Considering the rectangular face as base, 

area of rectangular base = 72 square inches

6x = 72

x = 72/6

x = 12 inches

Volume of the cuboid = 6 x 6 x 12

= 432 cubic inches

Example 9 :

A pyramid with a square base has a volume of 120 cubic meters and a height of 10 meters. Find the side length of the square base.

Solution :

Let x be the side length of square.

Volume of square base pyramid = 120 cubic meter

height = 10 meter

Area of base = area of square = x ⋅ x

x ⋅ x ⋅ 10 = 120

x² ⋅ 10 = 120

x² = 120/10

x² = 12

x = √12

x = 3.46

So, side length of square base is 3.46 meter.

Example 10 :

A pyramid with a square base has a volume of 912 cubic feet and a height of 19 feet. Find the side length of the square base.

Solution :

Let x be the side length of square.

Volume of square base pyramid = 912 cubcic feet

height = 9 feet

Area of base = area of square = x ⋅ x

x ⋅ x ⋅ 9 = 912

x² ⋅ 9 = 912

x² = 912/9

x² = 101.3

x = √101.3

x = 10.06

So, side length of square base is approximately 10.06 feet

Example 11 :

A pyramid with a rectangular base has a volume of 480 cubic inches and a height of 10 inches. The width of the rectangular base is 9 inches. Find the length of the rectangular base.

Solution :

Volume of pyramid = 480 cubic inches

height = 10 inches, width = 9 inches and length = x

10 ⋅ 9 ⋅ x = 480

90x = 480

x = 480/90

x = 5.33

So, side length of the rectangular base is 5.33 inches.

Example 12 :

A pyramid with a rectangular base has a volume of 105 cubic centimeters and a height of 15 centimeters. The length of the rectangular base is 7 centimeters. Find the width of the rectangular base.

Solution :

Volume of pyramid = 105 cubic cm

height = 15 cm, length = 7cm

let x be the width

7 ⋅ x ⋅ 15 = 105

105x = 105

x = 105/105

x = 1

So, width of the rectangular base is 1 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.