VOLUME OF TRIANGULAR PRISM

In a 3-D figure, if the base is a rectangle or square, two of the side walls side walls are triangles and other two side walls are rectangles or squares, then the 3-D figure is called triangular prism.

Any triangular prism will look like the one shown below.

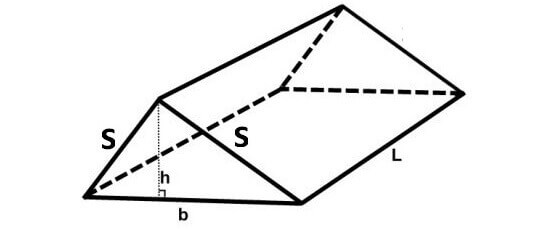
The formula to find volume of the above triangular prism is

= (1/2) x Base Area x Height

Important Note :

The above formula will work only if the given figure meets the following conditions.

(i) The base must be a rectangle or square.

(ii) Two of the side walls side walls must be triangles.

(iii) Other two side walls must be rectangles or squares.

Example 1 :

Find the volume of the prism.

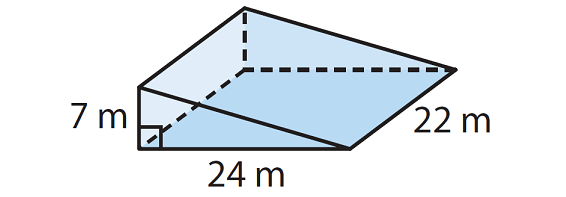
Solution :

Step 1 :

In the given prism, the base is  a rectangle, two of the side walls are triangles and other two side walls are rectangles.

So, the given prism is a triangular prism.

Step 2 :

Volume of a triangular prism = (1/2) x base area x height

V = (1/2) x B x h

Step 3 :

Find base area

Base Area = l x w

22 x 24

= 528 sq.m

Step 4 :

Find volume of the triangular prism

V = (1/2) x b x h

= (1/2) x (528) x 7

= 1848 cubic meters 

Example 2 :

Bradley’s tent is in the shape of a triangular prism shown below. How many cubic feet of space are in his tent ?

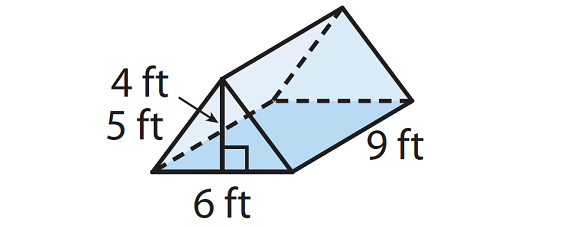
Solution :

Step 1 :

To find the number of cubic feet of space in Bradley’s  tent, we have to find the volume of his tent.

Step 2 :

Volume of a triangular prism = (1/2) x base area x height

V = (1/2) x b x h

Step 3 :

Find base area.

Base Area = l x w

= 9 x 6

= 54 sq.ft

Step 4 :

Find volume of the triangular prism.

V = (1/2) x b x h

= (1/2) x (54) x 4

= 108 cubic feet

Example 3 :

The figure is composed of a rectangular prism and a triangular prism. Find the volume of the figure.

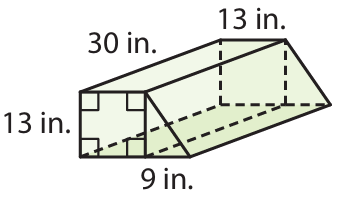
Solution :

Volume of the shape = volume of rectangular prism + volume of triangular prism

Volume of rectangular prism = length x width x height

Length = 30 inches, width = 13 inches and height = 13 inches

= 30 x 13 x 13

= 5070 cubic inches

volume of triangular prism = (1/2) x base x height x height of prism

base of triangle = 9 inches, height of triangle = 13 inches and height of prism = 30 inches

= (1/2) x 9 x 13 x 30

= 1755 cubic inches

Volume of the shape = 5070 + 1755

= 6825 cubic inches

Example 4 :

A solid glass paperweight is in the shape of a triangular prism The density of the glass is 2.4 g/cm³ Work out the mass of the paperweight.

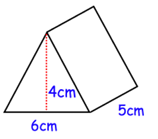
Solution :

density = mass / volume

mass = density x volume

base of triangle = 6 cm, height of triangle = 4 cm and height of prism = 5 cm

Volume = base area x height

= (1/2) x 6 x 4 x 5

= 60 cubic cm

Density = 2.4 g/cm³

mass = 2.4 x 60

= 144 grams

Example 5 :

Alex made a sketch for a homemade soccer goal he plans to build. The goal will be in the shape of a triangular prism. The legs of the right triangles at the sides of his goal measure 4 ft and 8 ft, and the opening along the front is 24 ft. How much space is contained within this goal

Solution :

In legs, base = 4 ft and height = 8 ft, height of prism = 24 ft

volume = base area x height

= (1/2) x 4 x 8 x 24

= 384 cubic ft

So, the space contained within this goal is 384 cubic ft.

Example 6 :

The volume of a square pyramid is 60 cubic inches and the height is 15 inches. Find the side length of the square base.

Solution :

Let x be the side lenght of square base.

volume = 60 cubic inches

base area x height = 60

x² x 15 = 60

x² = 60/15

x² = 4

x = 2

So, the side length of square is 2 inches.

Example 7 :

The volume of a square pyramid is 1024 cubic inches. The base has a side length of 16 inches. Find the height of the pyramid.

Solution :

Let h be the height of the pyramid

Volume of square pyramid = 1024 cubic inches

base area x height = 1024

16 x 16 x h = 1024

256 x h = 1024

h = 1024/256

h = 4 inches

So, height of the pyramid is 4 inches.

Example 8 :

Find the value of the variable in each figure. Leave answers in simplest radical form.

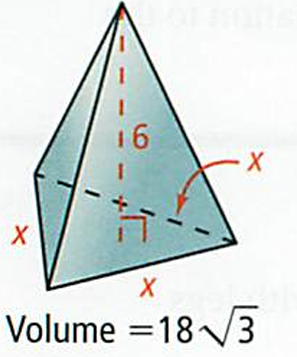
Solution :

By considering the base of the triangle, it is equilateral triangle.

Area of base = area of equilateral triangle = (√3/4) a²

Here a = side length = x

Volume of the shape = (√3/4) a² x height

18√3 = (√3/4) x² (6)

18√3 (4/√3)/6 = x²

 x² = 12

x = √12

x = √(2 ⋅ 2 ⋅ 3)

x = 2√3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.