VOLUME OF TRIANGULAR PRISM WORKSHEET

Question 1 :

Find the volume of the prism shown below.

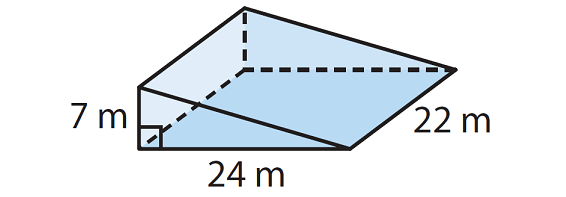
Step 1 :

In the given prism, the base is  a rectangle, two of the side walls are triangles and other two side walls are rectangles.

So, the given prism is a triangular prism.

Step 2 :

Volume of a triangular prism = (1/2) x base area x height

V = (1/2) x B x h

Step 3 :

Find base area

Base Area = l x w

22 x 24

= 528 sq.m

Step 4 :

Find volume of the triangular prism

V = (1/2) x b x h

= (1/2) x (528) x 7

= 1848 cubic meters

Question 2 :

Bradley’s tent is in the shape of a triangular prism shown below. How many cubic feet of space are in his tent ?

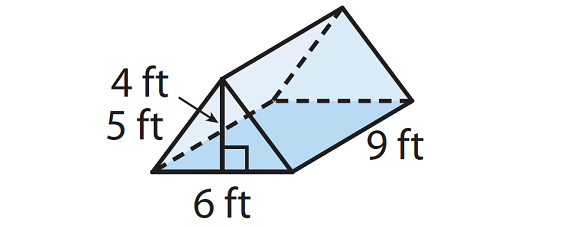
Solution :

Step 1 :

To find the number of cubic feet of space in Bradley’s  tent, we have to find the volume of his tent.

Step 2 :

Volume of a triangular prism = (1/2) x base area x height

V = (1/2) x b x h

Step 3 :

Find base area.

Base Area = l x w

= 9 x 6

= 54 sq.ft

Step 4 :

Find volume of the triangular prism.

V = (1/2) x b x h

= (1/2) x (54) x 4

= 108 cubic feet

Question 3 :

As a gift, you fill the calendar with packets of chocolate candy. Each packet has a volume of 2 cubic inches. Find the maximum number of packets you can fit inside the calendar.

Solution :

Volume of the calender = Base area x height of the prism

Base area = (1/2) x base x height

base = 4 inches and height = 6 inches

Height of the prism = 8 inches

= (1/2) x 4 x 6 x 8

= 2 x 6 x 8

= 96 cubic inches

Volume of one candy = 2 cubic inches

Then, the number of candies = 96/2

= 48 candies

Question 4 :

Lynette has a metal doorstop with the dimensions shown. Each cubic centimeter of the metal in the doorstop has a mass of about 8.6 grams. Find the volume of the metal in the doorstop. Then find the mass of the doorstop.

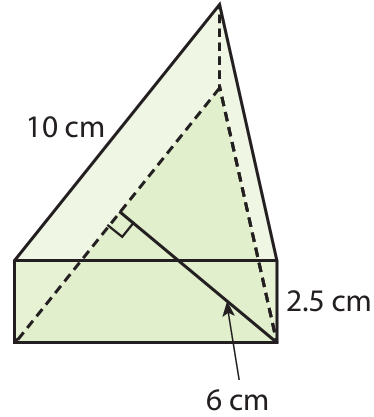
Solution :

Mass = 8.6 grams

Volume = (1/2) x base x height x height of the prism

= (1/2) x 10 x 6 x 2.5

= 5 x 6 x 2.5

= 75 cm³

1 cm³ = 1 g

Mass = 75 x 8.6

= 645 grams

Question 5 :

The volume of the triangular prism shown above is 160 cubic centimeters (cm³). What is the vertical height (h), in centimeters (cm), of the triangular base of the prism ?

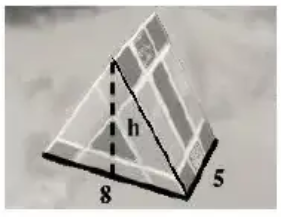
Solution :

Volume of triangular prism = 160 cubic cm

base of triangle = 8 cm, height of triangle = h cm

height of the prism = 5 cm

160 = (1/2) x 8 x h x 5

160 = 4 x h x 5

160 = 20h

h = 160/20

h = 8 cm

Question 6 :

The wodden door wedge has the shape of a right triangular prism as shown. The right triangular faces have a length of 1 = 10 cm and height of h = 4 cm. The prism has a width of w = 3 cm. What is the volume of door wedge in the cubic cm ?

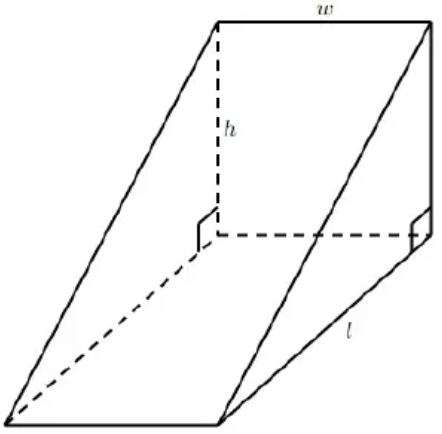
Area of triangular phase = (1/2) x base x height

base = 10 cm, height of triangle = 4 cm

height of prism = 3 cm

Volume = (1/2) x 10 x 4 x 3

= 5 x 4 x 3

= 60 cm³

Question 7 :

The right triangular prism with an equilateral triangular base is shown. The height of the right triangular prism is equal to 7 feet, and each side of the triangular base is equal to 5 ft. What is the volume of the right triangular prismm, rounded to the nerest cubic feet ?

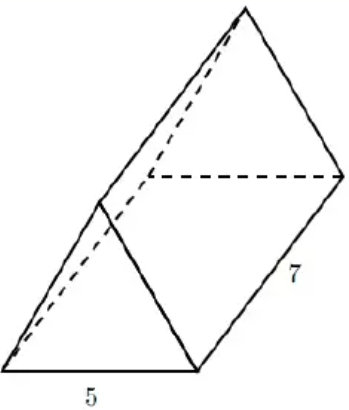
Area of equilateral triangle = (√3/4)a²

= (√3/4)(5²)

= (√3/4)(25)

= √3(6.25)

= 1.732 x 6.25

= 10.825 square feet

Volume of prism = base area x height

= 10.825 x 7

= 75.775 cubic feet

Question 8 :

A candy box shown at left is in the shape of a right triangular prism whose base is an equilateral triangle of side length s. For shipping and packing purposes the length l of the box must be 20 centimeters and the volume of the box must be 100 cubic centimeters. What is the side length (s) of the base of the box, rounded to the nearest tenth of a centimeter ? The volume V of a right triangular prism of length (l) and the base area A = V = Al.

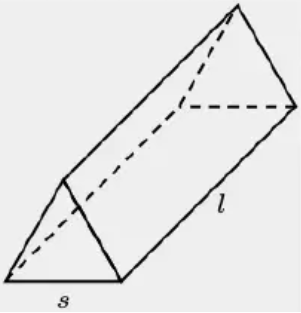
Solution :

Volume = 100 cubic cm

100 = A(10)

A = 100/10

Area of triangle = 10 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.