VOLUME OF RECTANGULAR PRISMS

Prism is basically a 3D shape. Even though we have different formulas to find volume of different kinds of prisms, the basic idea of finding volume is to multiply the base area and height of the prism.

A rectangular prism has six faces. Any pair of opposite faces can be called the bases of the prism. All the side walls are either rectangles or squares (that is, no side wall is triangle), then prism will look like as given below. 

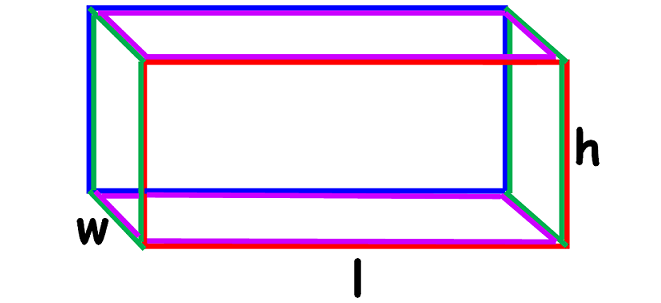
Volume of a rectangular prism is

= l x w x h

or

= Base Area x Height

Find the volume of the rectangular prism :

Example 1 :

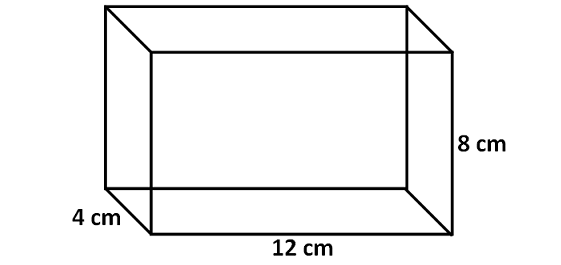
Solution :

We can find volume of the rectangular prism (cuboid) using the formula given below.

Base area x Height

Here, the base is a rectangle with length 12 cm and width 4 cm.

Area of the base is

= 12 x 4

= 48 cm²

Height of the cuboid is 8 cm.

So, volume of the above cuboid is

= 48 x 8

= 384 cm³

Example 2 :

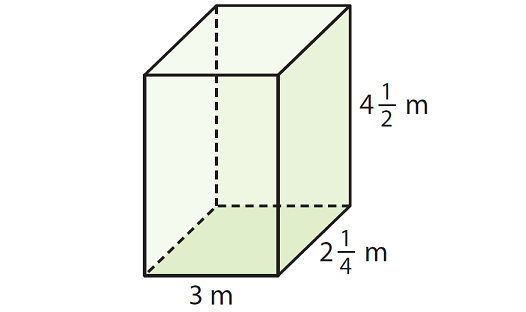
Solution :

We can find volume of the rectangular prism using the formula given below.

Base area x Height

Here, the base is a rectangle with length 3 m and width 2 1/4 m.

Area of the base is

= 3 x 2 1/4

= 3 x 9/4

= 27/4 m²

Height of the rectangular prism is 4 1/2 m.

So, volume of the above rectangular prism is

= 4 1/2  x 27/4

= (9/2)  x (27/4)

= 243/8

= 30 3/8 m³

Example 3 :

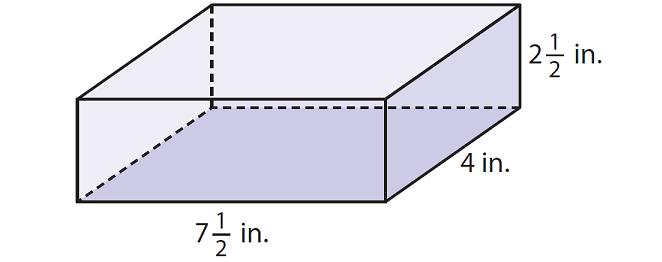
Solution :

We can find volume of the rectangular prism using the formula given below.

Base area x Height

Here, the base is a rectangle with length 7 1/2 inches and width 4 inches.

Area of the base is

= 7 1/2 x 4

= (15/2) x 4

= 30 in²

Height of the rectangular prism is 2 1/2 inches.

So, volume of the above rectangular prism is 

= 30 x 2 1/2

= 30  x 5/2

= 150/2

= 75 in³

Example 4 :

A cellular phone is in the shape of a rectangular prism. The height of the phone is 6 millimeters, and the width is 50 millimeters. The volume is 22,500 cubic millimeters. What is the length of the cellular phone?

Solution :

Height = 6 mm

Width = 50 mm

Volume = 22500 cubic mm

Let x be the side length of the cellular phone.

6(50)x = 22500

300x = 22500

x = 22500/300

x = 75

So, the length of the phone is 75 mm.

Example 5 :

A cube is made up of a group of smaller, identical cubes. The cube has a side length of three inches. What is the volume of one of the smaller cubes?

Solution :

Side length of given cube = 3 inches

Since the smaller cubes are identical, side length of one small cube = 1 inch

Volume of smaller cube = 1 inch

Volume of smaller cube = 1³

Example 6 :

A calendar that has one page per day is 7 inches long, 7 inches wide, and 2 inches high. What is the volume of one page of the calendar? Round your answer to the nearest thousandth.

Solution :

Length = 7 inches

Width = 7 inches and height = 2 inches

Volume = 7 (7) (2)

= 98 cubic inches.

Example 7 :

A terrarium is shaped like a rectangular prism. The prism is 25 1/2 inches long, 13 1/2 inches wide, and 16 inches deep. What is the volume of the terrarium?

Solution :

Length = 25  1/2 ==> 51/2 inches

Width = 13  1/2 ==> 27/2 inches

height = 16 inches

Volume of terrairum = (51/2) x (27/2) x 16

= 51 x 27 x 4

= 5508 cubic inches

Example 8 :

Each locker is shaped like a rectangular prism. Which has more storage space? Explain

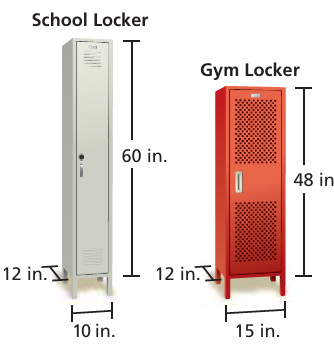
Solution :

Capacity of school locker = 60 x 12 x 10

= 7200 cubic inches

Capacity of gym locker = 48 x 12 x 15

= 8640 cubic inches

So, gym locker has more storage.

Example 9 :

A company is designing a juice box. The box is in the shape of a rectangular prism. The base of the box is 6 1/2 inches by 2 1/2 inches, and the box is 4 inches high. If juice fills 90% of the box’s volume, find the volume of juice in the box.

Solution :

Capacity of juice box = 6  1/2 x 2  1/2 x 4

= (13/2) x (5/2) x 4

= 13 x 5

= 65 cubic inches

90% of capacity = 90% of 65

= 0.90(65)

= 58.5 cubic inches

Example 10 :

Rectangular prism A measures 6 inches by 4 inches by 5 inches. Rectangular prism B’s dimensions are twice those of prism A. Find the volume of each prism. How many times as great is prism B’s volume as prism A’s volume?

Solution :

Volume of rectangular prism A = 6 x 4 x 5

= 120 cubic inches

Volume of rectangular prism B = 12 x 8 x 10

= 960 cubic inches

Number of times = 960/120

= 8 times

Volume of prims B is 8 times volume of prism A.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.