VOLUME OF RECTANGULAR PRISMS WORKSHEET

Find the volume of the rectangular prism :

Question 1 :

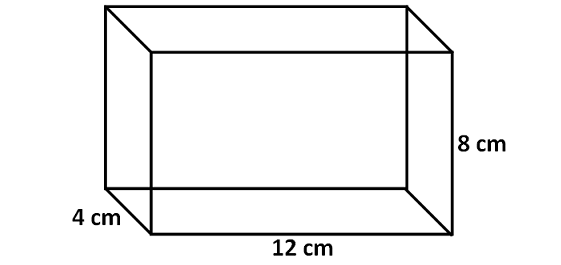
Solution :

We can find volume of the rectangular prism (cuboid) using the formula given below.

Base area x Height

Here, the base is a rectangle with length 12 cm and width 4 cm.

Area of the base is

= 12 x 4

= 48 cm²

Height of the cuboid is 8 cm.

So, volume of the above cuboid is

= 48 x 8

= 384 cm³

Question 2 :

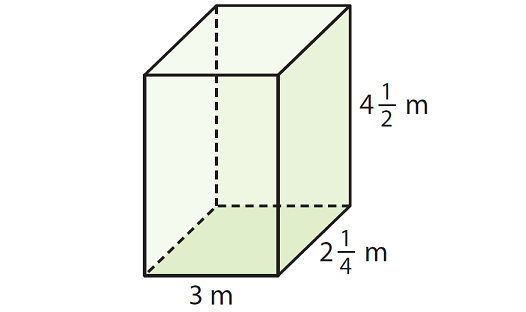
Solution :

We can find volume of the rectangular prism using the formula given below.

Base area x Height

Here, the base is a rectangle with length 3 m and width 2 1/4 m.

Area of the base is

= 3 x 2 1/4

= 3 x 9/4

= 27/4 m²

Height of the rectangular prism is 4 1/2 m.

So, volume of the above rectangular prism is

= 4 1/2  x 27/4

= (9/2)  x (27/4)

= 243/8

= 30 3/8 m³

Question 3 :

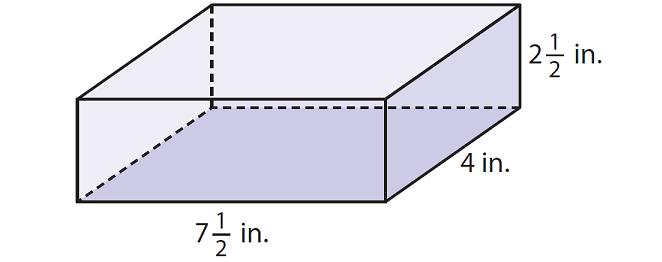
Solution :

We can find volume of the rectangular prism using the formula given below.

Base area x Height

Here, the base is a rectangle with length 7 1/2 inches and width 4 inches.

Area of the base is

= 7 1/2 x 4

= (15/2) x 4

= 30 in²

Height of the rectangular prism is 2 1/2 inches.

So, volume of the above rectangular prism is 

= 30 x 2 1/2

= 30  x 5/2

= 150/2

= 75 in³

Question 4 :

A rectangular fish tank measures 6.5 meters long, 4 meters wide, and 5 meters deep inside. If the tank is filled with 100 cubic meters of water, how much available space, in cubic meters, is left in the tank?

Solution :

Capacity of the tank = volume of rectangular prism

= 6.5 x 4 x 5

= 6.5 x 20

= 130 square meter

The difference between the capacity and quantity of water filled already

= 130 - 100

= 30 square meter.

So, the available space is 30 square meter.

Question 5 :

When completely filled, a rectangular tank at an aquarium holds 10,800 cubic yards of water. If the tank has a length of 36 yards and a height of 15 yards, what is the width of the tank?

Solution :

Capacity of the tank = 10800 cubic yards

Length of the tank = 36 yards

height = 15 yards

Let width be w

36 ⋅ 15 ⋅ w = 10800

w = 10800/(36 ⋅ 15)

= 20 yards

So, the width of the tank is 20 yards.

Question 6 :

You are trying to choose between 2 fish tanks. The dimension of the tanks are below. Which tank is largest ?

Solution :

Capacity of tank 1 = 30 x 20 x 15

= 9000 cm³

Capacity of tank 2 = 50 x 10 x 10

= 5000 cm³

Capacity of tank 1 is larger.

Question 7 :

Alexia's bathroom has a tub in the shape of a rectangular prism with the length of 72 inches, a width of 32 inches and the height of 20 inches. How many cubic inches of water can it hold ?

Solution :

Capacity of rectangular tub = length x width x height

= 72 x 20 x 32

= 46080 in³

So, capacity of the container is 46080 in³.

Question 8 :

One cubic foot of water weighs about 62.4 pounds. How many pounds of water can the fish tank hold when it is full?

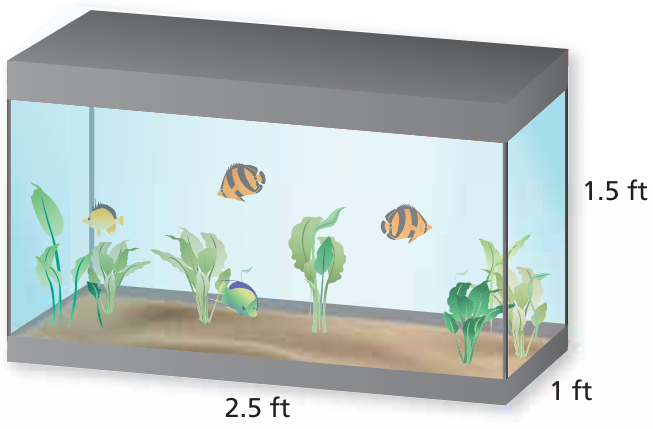
Solution :

1 cubic feet = 62.4 pounds

Capacity of fish tank = length x width x height

= 2.5 x 1 x 1.5

= 3.75 cubic feet

Capacity in pounds = 3.75 x 62.4

= 234 pounds

Question 9 :

a. Estimate the amount of casserole left in the dish.

b. Will the casserole fit in the storage container? Explain your reasoning.

Solution :

a)  length = 12 inches, width = 12 inches and height = 2  3/4 inches

Amount of casserole left in the dish

= 12 x 12 x 2  3/4

= 144 x (11/4)

= 36 x 11

= 396 cubic inches

b) Capacity of storage container = 4 x 7 x 7

= 196 cubic inches

So, quantity of casserole will not fit in the container.

Question 10 :

The area of the shaded face is 96 square centimeters. What is the volume of the rectangular prism

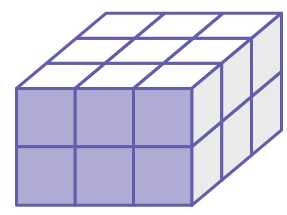
Solution :

Area of the shaded face = 96 square cm

By observing the figure, 

length = 3 cm, width = 3 and height = 2

Volume of rectangular prism

= area of the shaded portion x height of the prism

= 96 x 3

= 288 cubic cm

Question 11 :

One cubic foot of dirt weighs about 70 pounds. How many pounds of dirt can the dump truck haul when it is full?

Solution :

Find the volume of dirt that the dump truck can haul when it is full.

V = ℓwh 

= 17(8) (4 3/4)

= 646

So, the dump truck can haul 646 cubic feet of dirt when it is full.

To find the weight of the dirt,

multiply by 70 lb/1 ft³

646 ft³ × (70 lb/1 ft³) = 45,220 lb

The dump truck can haul about 45,220 pounds of dirt when it is full.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.