VOLUME OF PYRAMIDS AND CONES WORKSHEET

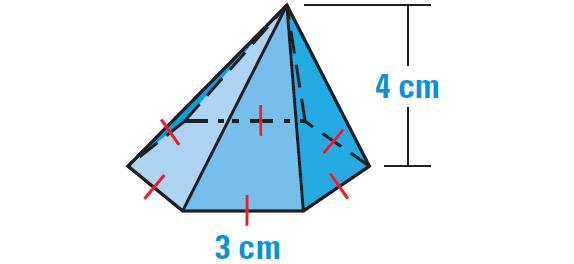
1. Find the volume of the pyramid with the regular base.

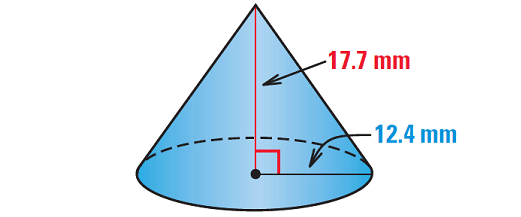
2. Find the volume of the right circular cone shown below.

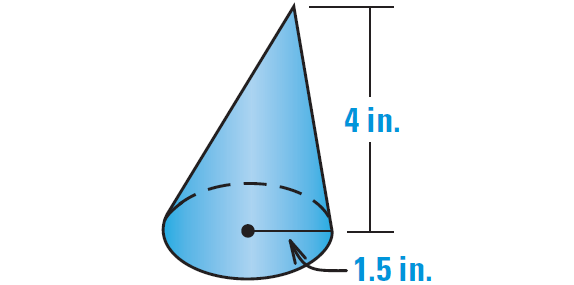
3. Find the volume of the oblique circular cone shown below.

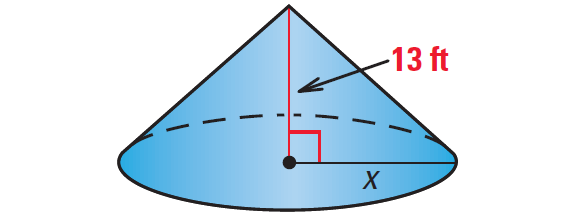
4. The volume of the right circular cone shown below is 2614 cubic feet. Find the value of x.

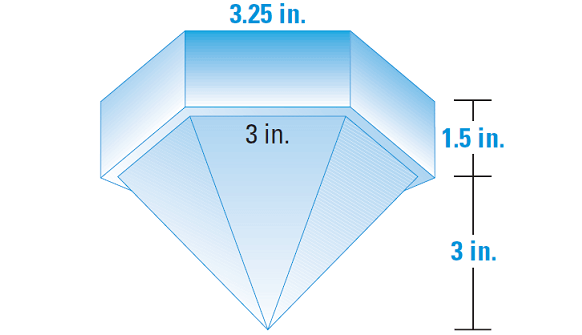
5. A nautical prism is a solid piece of glass, as shown. Find its volume.

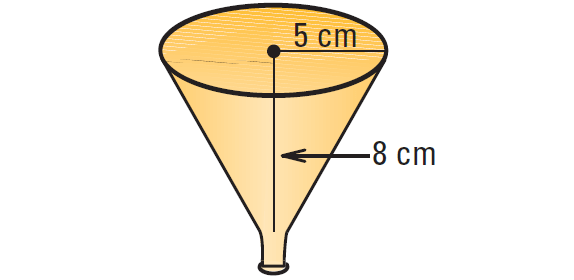
6. If oil is being poured into the funnel shown below at a rate of 147 milliliters per second and flows out of the funnel at a rate of 42 milliliters per second, estimate the time it will take for the funnel to overflow. (1 mL = 1 cm³).

Answers

1. Answer :

The base can be divided into six equilateral triangles as shown below.

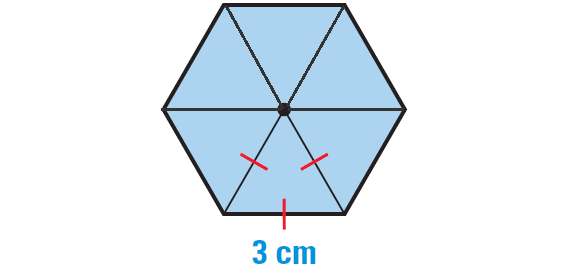
Using the formula for the area of an equilateral triangle, 

√3/4 ⋅ s²

the area of the base B can be found as follows :

B  =  6(√3/4 ⋅ s²)

Substitute 3 for s. 

B  =  6(√3/4 ⋅ 3²)

Simplify.

B  =  6(√3/4 ⋅ 9)

B  =  27√3 / 2  cm²

Formula for volume of a pyramid : 

V  =  1/3 ⋅ Bh

Substitute 27√3 / 2 for B and 4 for h. 

V  =  1/3 ⋅ (27√3 / 2)(4)

Simplify.

V  =  18√3

V  =  31.2

So, the volume of the pyramid is about 31.2 cubic centimeters.

2. Answer :

Formula for volume of a cone : 

V  =  1/3 ⋅ πr²h

Substitute 12.4 for r and 17.7 for h.

V  =  1/3 ⋅ π(12.4)²(17.7)

Simplify. 

V  =  907.184π

Use calculator. 

V  ≈  2850 mm³

So, the volume of the right circular cone is about 2850 cubic millimeters.

3. Answer :

Formula for volume of a cone : 

V  =  1/3 ⋅ πr²h

Substitute 1.5 for r and 4 for h.

V  =  1/3 ⋅ π(1.5)²(4)

Simplify. 

V  =  3π

Use calculator. 

V  ≈  9.42 in³

So, the volume of the oblique circular cone is about 9.42 cubic inches.

4. Answer :

Formula for volume of a cone : 

V  =  1/3 ⋅ πr²h

Substitute 2614 for V, x for r and 13 for h.

2614  =  1/3 ⋅ πx²(13)

Multiply each side by 3.

7842  =  13πx²

Divide each side by 13π.

7842/13π  =  x²

Find positive square root.

13.86  ≈  x

So, the value of x is about 13.86

5. Answer :

To find the volume of the entire solid, we have to add the volumes of the prism and the pyramid.

The bases of the prism and the pyramid are regular hexagons made up of six equilateral triangles.

To find the area of each base, B, multiply the area of one of the equilateral triangles by 6. 

That is, 6(√3/4 ⋅ s²), where s is the base edge. 

Let V₁ be the volume of prism and V₂ be the volume of pyramid.

Volume of Prism :

V₁  =  Bh

V₁  =  6(√3/4 ⋅ s²) ⋅ h

Substitute 3.25 for s and 1.5 for h. 

V₁  =  6[√3/4 ⋅ (3.25)²] ⋅ 1.5

Use calculator and simplify. 

V₁  ≈  41.166

Volume of Pyramid :

V₂  =  1/3 ⋅ 6(√3/4 ⋅ s²) ⋅ h

Substitute 3 for s and 3 for h. 

V₂  =  1/3 ⋅ 6(√3/4 ⋅ 3²) ⋅ 3

Use calculator and simplify. 

V₁  ≈  23.38

Volume of the Nautical Prism : 

V  =  V₁ + V₂

V  ≈  41.16 + 23.38

V  ≈  64.54  in³

So, the volume of the nautical prism is about 64.54 cubic inches.

6. Answer :

First, find the approximate volume of the funnel.

Because the funnel is in the shape of cone, we can use formula for volume of a cone to find volume of the funnel. 

V  =  1/3 ⋅ πr²h

Substitute 5 for r and 8 for h. 

V  =  1/3 ⋅ π(5²)(8)

Simplify.

V  =  1/3 ⋅ π(25)(8)

V  =  200π/3

Use calculator. 

V  ≈  209  cm³

Because, 1mL  =  1cm

V  ≈  209  mL

The rate of accumulation of oil in the funnel is

=  147 - 42

=  105 mL/s

To find the time it will take for the oil to fill the funnel, divide the volume of the funnel by the rate of accumulation of oil in the funnel as follows :

=  209 mL ÷ 105 mL/s

Simplify.

≈  2 seconds

So, the funnel will overflow after about 2 seconds.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.