VOLUME OF PRISMS AND CYLINDERS WORKSHEET

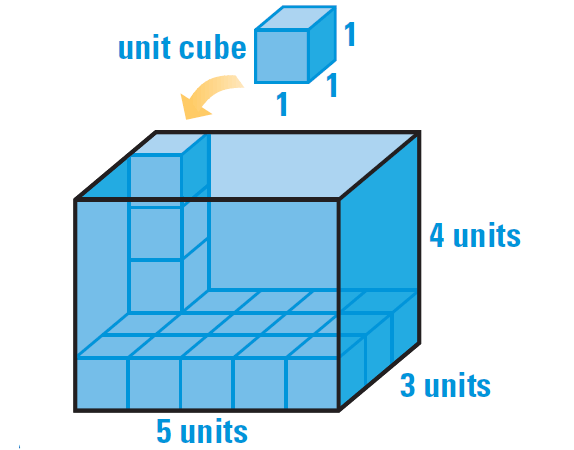
1. The box shown below is 5 units long, 3 units wide, and 4 units high. How many unit cubes will fit in the box ? What is the volume of the box ?

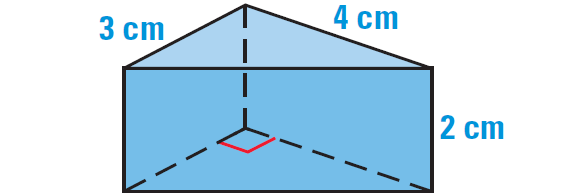
2. Find the volume of the right prism shown below.

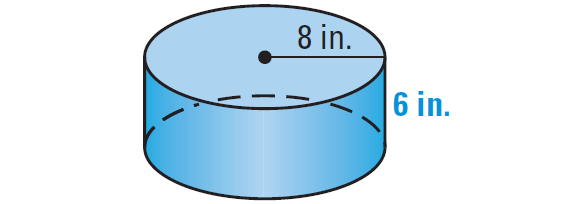
3. Find the volume of the right cylinder shown below.

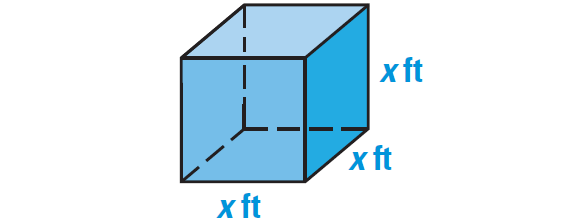
4. The volume of the cube shown below is 100 ft³. Find the value of x. 

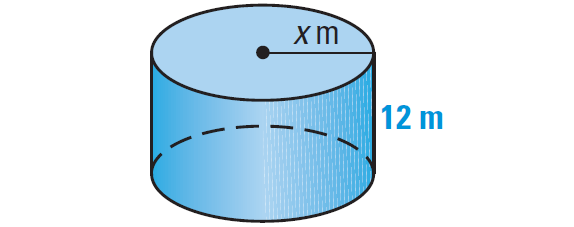
5. The volume of the right cylinder shown below is 4561 m³. Find the value of x. 

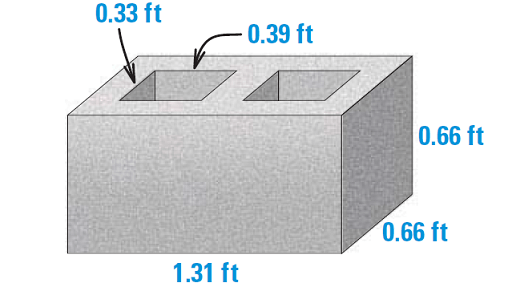
6. If a concrete weighs 145 pounds per cubic foot, find the weight of the concrete block shown below. 

Answers

1. Answer :

The base of the box is 5 units by 3 units. This means 5 • 3 or 15 unit cubes, will cover the base.

Solution (a) :

Three more layers of 15 cubes each can be placed on top of the lower layer to fill the box. Because the box contains 4 layers with 15 cubes in each layer, the box contains a total of 4 • 15, or 60 unit cubes.

Solution (b) :

Because the box is completely filled by the 60 cubes and each cube has a volume of 1 cubic unit, it follows that the volume of the box is 60 • 1, or 60 cubic units.

2. Answer :

The area of the base is 

B  =  1/2 ⋅ (3)(4)

B  =  6 cm²

The height is 

h  =  2 cm

Formula for volume of a right prism is 

V  =  Bh

Substitute 6 for B and 2 for h. 

V  =  (6)(2)

V  =  12

So, the volume of the right prism is 12 cubic cm. 

3. Answer :

Formula for volume of a right cylinder is

V  =  πr²h

Substitute 8 for r and 6 for h. 

V  =  π(8²)(6)

Simplify. 

V  =  384π

Use calculator. 

V  ≈  1206.37

So, the volume of the right cylinder is about 1206.37 cubic inches. 

4. Answer :

A side length of the cube is x feet. 

Formula for volume of a cube : 

V  =  s³

Substitute 100 for V and x for s. 

100  =  x³

Take cube root on both sides. 

∛100  =  ∛x

4.64  ≈  x

So, the value of x is about 4.64

5. Answer :

Formula for volume of a right cylinder is

V  =  πr²h

Substitute 4561 for V, x for r and 12 for h. 

4561  =  πx³(12)

4561  =  12πx³

Divide each side by 12π. 

4561/12π  =  x²

Find the positive square root. 

11  ≈  x

So, the value of x is about 11.

6. Answer :

To find the weight of the concrete block shown, we need to find its volume.

The area of the base can be found as follows :

B  =  Area larger rectangle - 2 ⋅ Area of small rectangle

B  =  (1.31)(0.66) - 2(0.33)(0.39)

B  ≈  0.61 ft²

Using the formula for the volume of a prism, the volume is

V  =  Bh

V  ≈   0.61(0.66)

V  ≈  0.40 ft³

To find the weight of the block, multiply the pounds per cubic foot, 145 lb/ft³, by the number of cubic feet, 0.40 ft³.

Weight  =  [145 lb/ft³] ⋅ [0.40 ft³]

Simplify.

Weight  ≈  58 lb

So, the weight of the concrete block is about 58 pounds.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.