VOLUME OF CUBOID WORD PROBLEMS

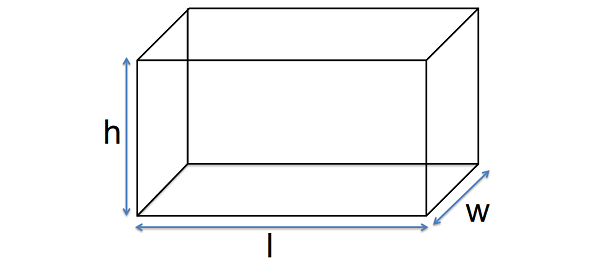
If the length, width and height of a cuboid are l, w and h respectively, then

volume  of the cuboid = l x w x h cubic units

Problem 1 :

The length, breadth and depth of a pond are 20.5 m, 16 m and 8 m respectively. Find the capacity of the pond in liters.

Solution :

l = 20.5 m, w = 16 m, h = 8 m

Capacity of pond :

= l x w x h

= 20.5 (16) (8)

= 2624 m³

1 m³ = 1000 liters

= 2624(1000) liters

= 2624000 liters

Problem 2 :

The dimensions of a brick are 24 cm x 12 cm x 8 cm. How many such bricks will be required to build a wall of 20 m length, 48 cm breadth and 6 m height?

Solution :

Volume of 1 brick :

= l x w x h

= 24(12)(8)

  = 2304 cm³

Dimensions of the wall :

l = 20 m = 2000 cm

w = 48 cm

h = 6 m = 6000 cm

Volume of wall :

= l x w x h

= 2000(48)(600)

= 57600000 cm³

Number of bricks required :

= 57600000/2304

= 25000

Problem 3 :

The volume of a container is 1440 m³. The length and width of the container are 15 m and 8 m respectively. Find its height

Solution :

Volume of container = 1440 m³

length x width x height = 1440

15 x 8 x h = 1440

height = 1440/120

height = 12 m

Problem 4 :

The side of a metallic cube is 12 in. It is melted and formed into a cuboid whose length and width are 18 in and 16 cm respectively. Find the height of the cuboid.

Solution :

volume of cuboid = volume of cube

l x w x h = a³

18 x 16 x h = 12³

288h = 1728

Divide both sides by 288.

h = 6 in

Problem 5 :

The length, width and height of a cuboid are in the ratio 7 : 5 : 2. Its volume is 35840 cm³. Find its dimensions.

Solution :

From the ratio 7 : 5 : 2, the dimensions of the cuboid are

length = 7x, width = 5x, height = 2x

Volume = 35840 cm³

(7x)(5x)(2x) = 35840

70x³ = 35840

Divide each side by 70.

x³ = 512

x³ = 8³

x = 8

Length = 7(8) = 56 cm

Width = 5(8) = 40 cm

Height = 2(8) = 16 cm

Problem 6 :

The diagram shows the dimensions of a standard gold bar at Fort Knox. Gold has a density of 19.3 grams per cubic centimeter. Find the mass of a standard gold bar to the nearest gram.(1 cubic inch = 16.38706 gram)

Solution :

Length of gold bar = 7 inches

width = 3.625 inches

height = 1.75 inches

Volume of gld bar = length x width x height

= 7 x 3.625 x 1.75

= 44.40625 cm³

Given that, 1 cubic inch = 16.38706 gram)

= 44.40625 x 16.38706

= 727.68 grams

density = 19.3 grams

mass = volume x density

= 727.68 x 19.3

= 14044.224 grams

1000 gram = 1 kg

= 14044.224/1000

= 14.04 kg

Problem 7 :

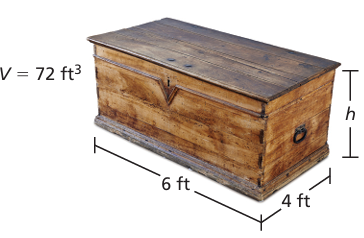
You are building a rectangular chest. You want the length to be 6 feet, the width to be 4 feet, and the volume to be 72 cubic feet. What should the height be?

Solution :

Volume = 72 cubic feet

length = 6 ft, width = 4 ft and height = ?

6 x 4 x h = 72

h = 72/24

h = 3 ft

So, the required height is 3 ft.

Problem 8 :

You are building a 6-foot-tall dresser. You want the volume to be 36 cubic feet. What should the area of the base be? Give a possible length and width.

Solution :

Volume = 36 cubic feet

length = ?,  width = ? and height = 6

l x w x 6 = 36

l x w = 36/6

l x w = 6 ft

length = 2 ft and width = 3 ft..

Problem 9 :

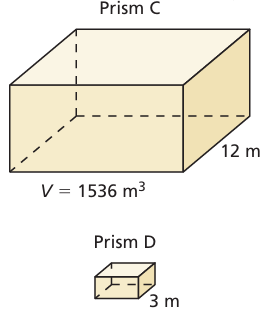
Prism C and prism D are similar. Find the volume of prism D.

Solution :

When two prisms are similar,

volume of prism C / volume of prism D = (ratio of corresponding sides)³

1536/volume of prism D = (12/3)³

1536/volume of prism D = 4³

1536/volume of prism D = 64

Volume of prism D = 1536 / 64

= 24 m³

So, the required volume of prism D is 24 m^3. 

Problem 10 :

An aquarium shaped like a rectangular prism has a length of 30 inches, a width of 10 inches, and a height of 20 inches. You fill the aquarium 3/4 full with water. When you submerge a rock in the aquarium, the water level rises 0.25 inch.

a. Find the volume of the rock.

b. How many rocks of this size can you place in the aquarium before water spills out?

Solution :

Capacity of water in aquarium = length x width x height

= 30 x 10 x 20

= 6000 cubic inches

3/4 of its capacity = 3/4 x 6000

= 3 x 1500

= 4500

Volume of rock which is submerge = volume of water level raises with the height of 0.25 inch

= length x width x 0.25

= 30 x 10 x 0.25

= 75 cubic inches

b) When wight of rock is more than the capacity of water in the tank, the water will flow out.

Quantity of water to be filled to make the tank full

= 6000 - 4500

= 1500

= 1500/75

= 20 rocks

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.