VOLUME OF COMPOSITE SOLIDS WORKSHEET

Problem 1 :

Allie has two aquariums connected by a small square prism. Find the volume of the double aquarium.

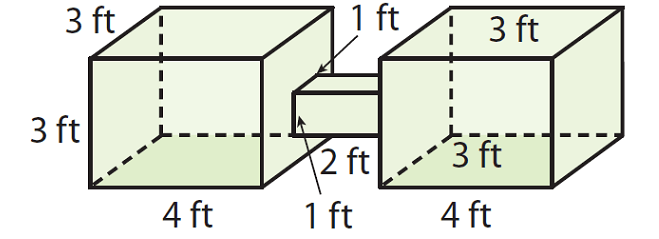
Solution :

Step 1 :

Find the volume of each of the larger aquariums.

Volume  =  Base area x Height

Volume  =  (4 x 3) x 3

Volume  =  12 x 3

Volume  =  36 cubic ft. 

Step 2 :

Find the volume of the connecting prism.

Volume  =  Base area x Height

Volume  =  (2 x 1) x 1

Volume  =  2 x 1

Volume  =  2 cubic ft.

Step 3 :

Add the volumes of the three parts of the aquarium.

V  =  36 + 36 + 2

V  =  74 cubic ft.

The volume of the aquarium is 74 cubic ft.

Problem 2 :

The figure is composed of a rectangular prism and a triangular prism. Find the volume of the figure.

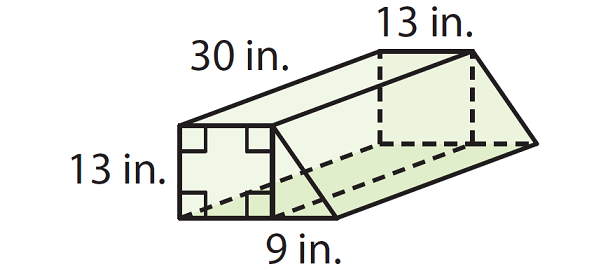
Solution :

Step 1 :

Find the volume of each of the larger aquariums.

Volume  =  Base area x Height 

Volume  =  (30 x 13) x 13

Volume  =  5070 cubic in.

Step 2 :

Find the volume of the triangular prism.

Volume  =  (1/2) x Base area x Height 

Volume  =  (1/2) x (30 x 9) x 13

Volume  =  1755 cubic in.

Step 3 :

Add the volumes of the two parts of the aquarium.

V  =  5070 + 1755

V  =   6825 cubic in.

The volume of the given figure is 6825 cubic in.

Problem 3 :

The figure is composed of a rectangular prism and a triangular prism. Find the volume of the figure.

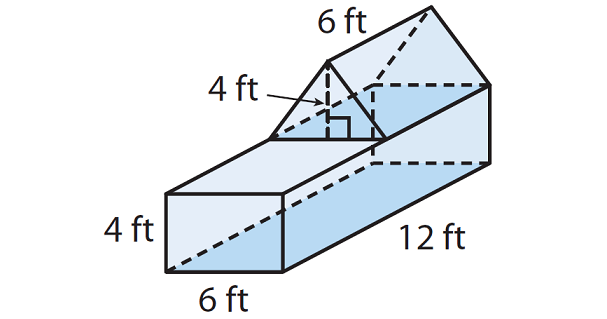
Solution :

Step 1 :

Find the volume of each of the larger aquariums.

Volume  =  Base area x Height 

Volume  =  (12 x 6) x 4

Volume  =  288 cubic ft.

Step 2 :

Find the volume of the triangular prism.

Volume  =  (1/2) x Base area x Height 

Volume  =  (1/2) x (6 x 6) x 4

Volume  =  72 cubic ft.

Step 3 :

Add the volumes of the two parts of the aquarium.

V  =  288 + 72

V  =   360 cubic ft.

The volume of the given figure is 360 cubic ft.

Problem 4 :

A snack stand serves a small order of popcorn in a cone-shaped container and a large order of popcorn in a cylindrical container.

a. How many small containers of popcorn do you have to buy to equal the amount of popcorn in a large container? Explain.

b. Which container gives you more popcorn for your money? Explain.

Solution :

Capacity of popcorn = (1/3)πr²h

r = 1.3 inches and height = 8 inches

= (1/3) x 3.14 x 1.3² x 8

= 14.15 cubic inches

Capacity of pop corn = πr²h

r = 1.3 inches and height = 8 inches

= 3.14 x 1.3² x 8

= 42.45 cubic inches

Amount of pop corn in the cylindrical container is greater than the amount of popcorn in the conical container is lesser.

a)  Number of smaller containers needed

= 42.45/14.15

= 3

So, 3 small containers are needed.

b)  The cylindrical container will have more quantity of popcorn.

Problem 5 :

The traffic cone is approximately a right cone with a radius of 2 1/2 inches and a height of 12 inches. Find the volume of the traffic cone to the nearest cubic inch.

Solution :

Radius = 2  1/2 inches

= 5/2 inches

height = 12 inches

Volume of traffic cone = (1/3)πr²h

= (1/3) x 3.14 x 2.5² x 12

= 3.14 x 2.5 x 2.5 x 4

= 78.5 cubic inches

Problem 6 :

A cat eats half a cup of food, twice per day. Will the automatic pet feeder hold enough food for 10 days? Explain your reasoning. (1 cup ≈ 14.4 in.3)

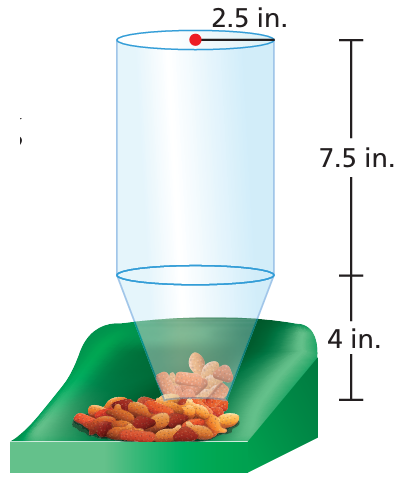
Solution :

Capacity of food hold by the automatic pet feeder 

= πr²h + (1/3) πr²h

Height of cylinder = 7.5 inches

height of cone = 4 inches

Radius of cylinder = cone = 2.5 inches

= π[2.5² x 7.5 + (1/3) 2.5²  x 4]

= 3.14 [46.875 + 8.33]

= 3.14 x 55.2

= 173.28 cubic inches

1 cup of food = 14.4 cubic inches

Half cup twice per day, which means one cup each day.

10 cups of food = 14.4 x 10

= 144 cups of food

Since the automatic feeder has the capacity of 173.28 cubic inches. This food will be enough.

Problem 7 :

During a chemistry lab, you use a funnel to pour a solvent into a flask. The radius of the funnel is 5 centimeters and its height is 10 centimeters. You pour the solvent into the funnel at a rate of 80 milliliters per second and the solvent flows out of the funnel at a rate of 65 milliliters per second. How long will it be before the funnel overflows? (1 mL = 1 cm³)

Solution :

V = 1/3(π x r²h)

where r is the radius and h is the height of the cone.

Given a funnel is getting filled with the solvent at a rate of 80ml per sec and the solvent is coming out of the funnel at a rate of 65ml per sec.

rate at which the funnel is getting filled is 80-65 = 15 ml per sec.

So, this means that the funnel is getting filled at a rate of 15ml per sec.

For the funnel to overflow it need to be filled completely.

The time before the funnel gets overflowed is

= volume of funnel/ rate

A funnel is in the shape of an inverted cone.

The volume of the funnel V = 1/3(π x r²h)

V = 1/3 (3.14 * 5² * 10)

V = 1/3 (785.7)

V = 261.8ml³

Time before the funnel gets overflowed is 261.8/15

= 17.45 Sec

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.