VOLUME OF  A TRAPEZOIDAL PRISM

Example 1 :

Find volume of the prism shown below.

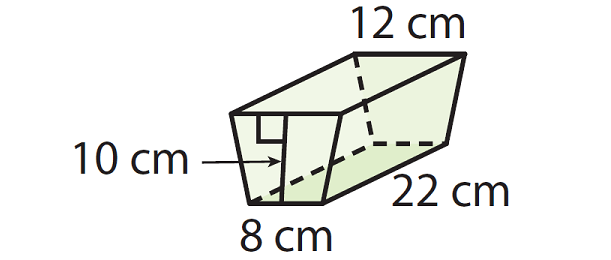
Solution :

Step 1 :

In the given prism, the two side walls are trapezoids. If we consider one of the trapezoid side walls as base, the height of the prism would be 22 cm.

So, the given prism is a trapezoidal prism.

Step 2 :

Volume of the given prism is

= base area x height

or

V = B x h

Step 3 :

Find base area.

Area of trapezoid with bases of lengths b₁ and b₂ and height h.

Base area (B) = (1/2) x (b₁ + b₂)h

= (1/2) x (12 + 8)10

= 100 sq.cm

Step 4 :

Find volume of the prism. 

V = B x h

= 100 x 22

= 2200 cubic cm

The volume of the given prism is 2200 cubic cm.

Example 2 :

Cherise is setting up her tent. Her tent is in the shape of a trapezoidal prism shown below. How many cubic feet of space are in her tent ?

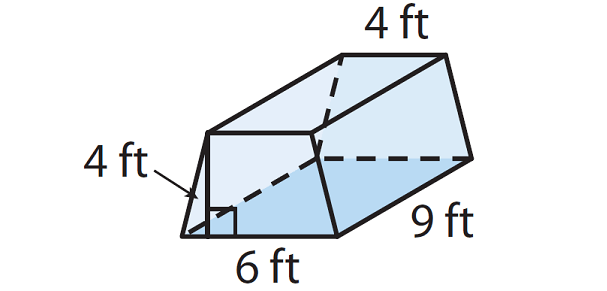
Solution :

Step 1 :

To find the number of cubic feet of space in  the tent, we have to find the volume of Cherise's tent.

Step 2 :

Volume of Cherise's tent (Trapezoidal prism) is

  = base area x height

or

V = B x h

Step 3 :

Find base area.

Area of trapezoid with bases of lengths b₁ and b₂ and height h.

Base area (B) = (1/2) x (b₁ + b₂)h

= (1/2) x (6 + 4)4

= 20 sq.ft

Step 4 :

Find volume of the prism.

V = B x h

= 20 x 9

= 180 cubic.ft

So, the number of cubic feet of space in  Cherise's tent is 180.

Example 3 :

The shape of the box for a chocolate treat is a hexagonal prism, as shown below. Each box has a volume of 227 cm³. For Christmas, the company will switch to a festive box in the form of a hexagon-based pyramid. This festive box, which is intended to be stood upright and portray a Christmas tree, will have the same base and height as the standard prism packaging.

a) Determine the volume of the festive box. Round your answer to two decimal places.

b) If the treat usually costs $6.99, what would be a reasonable price for the festive version?

Solution :

a)

Volume of festive box = (1/3) x base area x height

= 1/3 x 227

= 75.66

So, volume of festive box is 75.66 cm³

b) The standard box costs $6.99. A reasonable price for the festive box should be proportional to its volume, so the cost of the festive box would be one-third of the standard price.

Price of festive box = 1/3 x 6.99

= $2.33

Given that the festive box contains one-third the amount of product, a reasonable price would be $2.33.

Example 4 :

Nautical deck prisms were used as a safe way to illuminate decks on ships. The deck prism shown here is composed of the following three solids: a regular hexagonal prism with an edge length of 3.5 inches and a height of 1.5 inches, a regular hexagonal prism with an edge length of 3.25 inches and a height of 0.25 inch, and a regular hexagonal pyramid with an edge length of 3 inches and a height of 3 inches. Find the volume of the deck prism.

Solution :

Volume of first regular hexagonal prism = base area x height

base area of hexagonal = (1/2) x perimeter x apothem

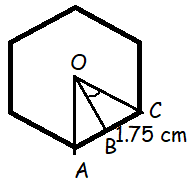
Finding apothem :

tan 30 = BC/OB

1/√3 = 1.75/OB

OB = 1.75√3

= (1/2) x 6(3.5) x 1.75√3

= 3 x 3.5 x 1.75 x 1.732

= 31.825

Height of the prism = 1.5 inches

Volume = 31.825 x 1.5

= 47.73 cubic inches

Volume of other hexagonal prism :

tan 30 = BC/OB

Half of side length = 3.25/2

= 1.625

1/√3 = 1.625/OB

OB = 1.625√3

= (1/2) x 6(3.25) x 1.625√3

= 3 x 3.25 x 1.625 x 1.732

= 27.44

Height of the prism = 0.25 inches

Volume of prism = 27.44 x 0.25

= 6.86 cubic inches

Volume of hexagonal pyramid :

tan 30 = BC/OB

1/√3 = 1.5/OB

OB = 1.5√3

= (1/2) x 6(3) x 1.5√3

= 3 x 3 x 1.5 x 1.732

= 23.38

Height of the prism = 3 inches

Volume = (1/3) x 23.38 x 3

= 23.38 cubic inches

Total volume = 47.73 + 6.86 + 23.38

= 77.97 cubic inches

So, the required volume is approximately 78 cubic inches.

Example 5 :

In the diagram below, the pyramid has a volume of 12.5 m³. Determine the volume of the prism (both solids have the same base and height).

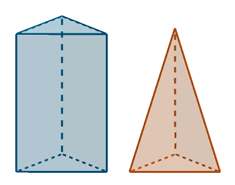
Solution :

Volume of prism = base area x height

Volume of pyramid = (1/3) x base area x height

Here both pyramid and prism has same base. So, base area will be the same.

12.5 = (1/3) x base area x height

base area x height = 12.5(3)

= 37.5 m³

So, volume of prism is 37.5 m³.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.