VOLUME OF A CONE WORD PROBLEMS

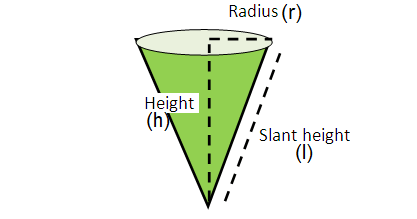
The formula to find the volume of a cone is given by

V = 1/3 · πr²h cubic units

Problem 1 :

The height and diameter of a cone-shaped storage tank are 9 feet and 14 feet respectively. Find the volume of liquid the tank can hold. Round your answer to the integer, if necessary. Use the approximate of value of π, that is 3.14. 

Solution : 

Step 1 : 

Because the tank is in the shape of cone, we can use the formula of volume of a cone to find volume of water the tank can hold.

Write the formula to find volume of a cone.

V  =  1/3 · πr²h -----(1)

Step 2 : 

To find the volume, we need the radius of the cone. But, the diameter is given, that is 14 ft. So, find the radius. 

r  =  diameter / 2

r  =  14/2

r  =  7

Step 3 : 

Substitute π ≈ 3.14, r = 7 and h = 9 in (1).

V  ≈  1/3 · 3.14 · 7² · 9

Simplify.

V  ≈  1/3 · 3.14 · 49 · 9

V  ≈  461.58

Round it to the nearest integer.

V  ≈  462

So, the volume of the clay is about 462 cubic inches.

Problem 2 :

A silo is shaped like a cone and contains wheat. The radius is 10 feet and the height is 15 feet. If the silo can release wheat from its bottom at the rate of 25 cubic feet per minute, how long would it take for the silo to empty fully ? Round your answer to the nearest minute. Use the approximate of value of π, that is 3.14. 

Solution : 

Step 1 : 

To know how long it would take for the silo to empty fully, first we have to find the volume of wheat in the silo.

Because the silo is in the shape of cone, we can use the formula of volume of a cone to find volume of wheat the tank can hold.

Write the formula to find volume of a cone.

V  =  1/3 · πr²h -----(1)

Step 2 : 

Substitute π ≈ 3.14, r = 10 and h = 15 in (1).

V  ≈  1/3 · 3.14 · 10² · 15

Simplify.

V  ≈  1/3 · 3.14 · 100 · 15

V  ≈  1,570

So, the volume of wheat in the silo is about 1,570 feet. 

Step 3 : 

Silo can release wheat from its bottom at the rate of 25 cubic feet per minute. 

To know how long it would take for the silo to empty 1,570 cubic feet of wheat, divide 1,570 by 25. 

=  1,570 / 25

=  62.8

  ≈  63

So, it would take about 63 minutes for the silo to empty fully.

Problem 3 :

You have 10 gallons of lemonade to sell. (1 gal ≈ 3785 cm³)

a. Each customer uses one paper cup. How many paper cups will you need?

b. The cups are sold in packages of 50. How many packages should you buy?

c. How many cups will be left over if you sell 80% of the lemonade?

Solution :

a)

1 gallon = 3785 cm³

10 gallons = 10 x 3785

= 37850 cm³

Capacity of paper cup = 1/3 · πr²h

radius = 4 cm and height = 10 cm

= 1/3 · π(4)²(10)

= 167.46 cm³

Number fo cups needed = 37850/167.46

= 226.02

Approximately 226 paper cups

b) One package will consists of 50. 

To get 226, number of packages should buy = 226/50

= 4.52

approximately 5 packages.

c)  80% of lemonade = 80% of 37850

= 0.80(37850)

= 30280 cm³

number cups needed to sale 30280 cm³ cup of lemanode

= 30280/167.46

= 180.8

approximately 181 cups.

Remianing number of cups = 226 - 181

= 45 cups

Problem 4 :

If a cone  shaped hole is 3 feet deep and the circumference of the base of the hole is 44 feet. What is the volume of the hole ?

Solution :

Circumferece of base = 44 feet

2πr = 44

height of cone = 3 feet

2 x 22/7 x r = 44

r = (44 x 7)/44

r = 7

Volume fo cone = 1/3 · πr²h

= 1/3 · (22/7) x 7²x 3

= 22 x 7

= 154 ft³

So, the volume of the hole is 154 ft³.

Problem 5 :

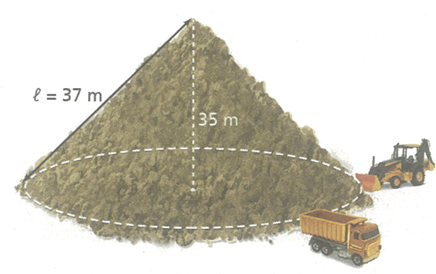
A city engineer determines that 5500 cubic meters of sand will be needed to treat the roadways this winter. Does the city have enough sand to treat the roadways ?

Solution :

r = ?, slant height (l) = 37 m and height (h) = 35 m

r = √l² - h²

= √37² - 35²

= √144

r = 12 m

Quantity of sand = 1/3 · πr²h

= 1/3 · (22/7) x 12² x 35

= 110880/21

= 5280 m³

Quantity of sand required = 5500 cubic meter

So, the sand is enough.

Problem 6 :

A water tank is shaped line a cone shown.

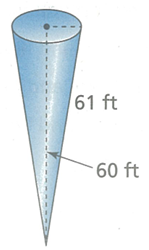
a) How much water the tank hold.

b) If water is drained from the tank to fill smaller tanks that each hold 500 cubic feet of water, how many smaller tanks can be filled ?

Solution :

a) Capcacity of water the tank hold = 1/3 · πr²h

Slant height = 61 ft and height (h) = 60 ft

r = √l² - h²

r = √61² - 60²

= √3721 - 3600

= √121

r = 11 ft

= 1/3 · π(11)²(60)

= 7598.8 cubic feet

b)

Each smaller tank can hold = 500 cubic feet

number of tanks = 7598.8/500

= 15.19

= 15 tanks

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.