VOLUME OF 3D SHAPES

Trace the outline of a $1 coin, $100 note and a square cookie on a paper.

What shapes have you traced?

A circle, a rectangle and a square. Isn’t it? Th ese shapes represents the plane figures. Also, these plane figures have two dimensions namely length and width. Now, you place some one dollar coins, some $100 notes and some square shaped cookies respectively on the drawn shapes as shown below.

What do you get now?

A cylinder, a cuboid and a cube. Isn’t it? Th ese shapes do not lie completely on the plane and they occupy some space also. Th at is, they have the third dimension namely the height along with the dimensions length and breadth. Th us, the shapes which have three dimensions namely length, breadth and height (depth) are called three dimensional shapes, simply called as 3-D shapes.

Some examples of 3-D shapes :

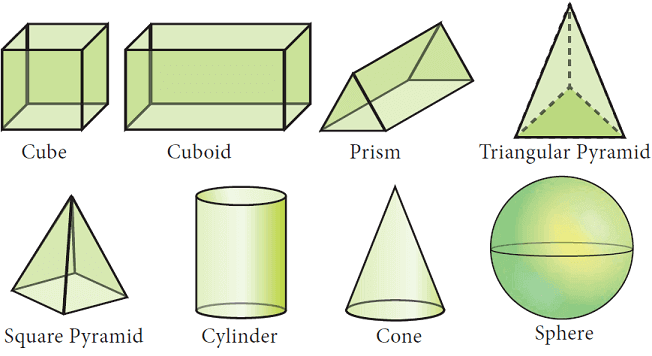
To find volume of any 3-D shape, we have to multiply the base area and height. Based on this, we can find the area of 3-D shapes like cylinder, cone, sphere etc.

Volume of a 3-D Shape = Base Area x Height

Example :

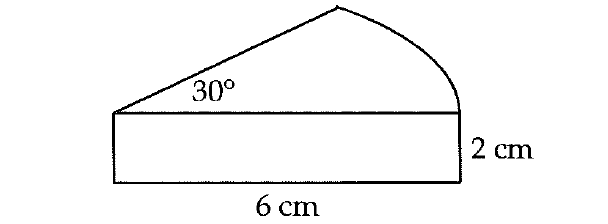
A wedge formed by a central angle of 30° as shown above was cut from a circular block of cheese with a radius of 6 cm and a thickness of 2 cm. What is the volume, in cubic centimeters, of the wedge?

Answer :

To find the volume of the wedge, we have to multiply the base area and height. Here, the base is a sector. So, we can find the area of the base using sector formula.

Area of the base = (θ/360°)(πr²)

Substitute θ = 30° and r = 6.

Area of the base = (30°/360°)(π ⋅ 6²)

= (1/12)(36π)

= 3π cm²

 Volume of the wedge = Area of the base x Height

= 3π cm² x 2 cm

= 6π cm³

When we are trying to find volume of 3-D shapes like cubes, cuboids, prisms and pyramids, we have to consider the following important points.

1. Let the base of a prism be a rectangle or square. If all the side walls are either rectangles or squares (that is, no side wall is triangle), then prism will look like as given below. 

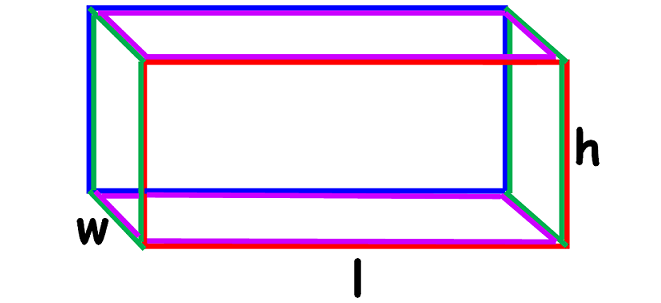
The formula to find volume of the above prism 

= Base Area x Height

2. Let the base of a prism be a rectangle or square. If two of the side walls side walls are triangles and other two side walls are rectangles or squares, then prism will look like as given below. 

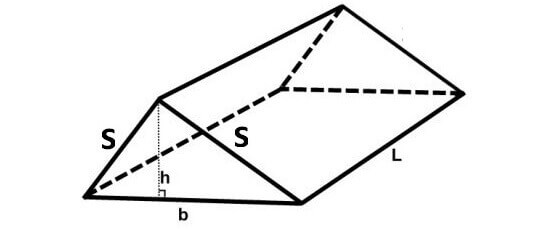
The formula to find volume of the above prism 

= (1/2) x Base Area x Height

3. Let the base of a prism be a triangle. If all of the side walls are rectangles or squares, then the prism will look like as given below.  

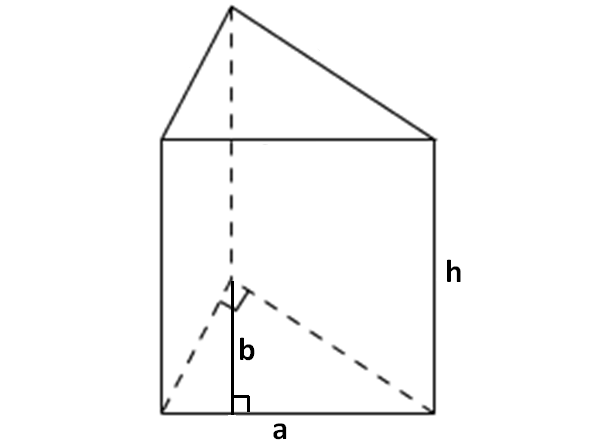
The formula to find volume of the above prism 

= Base Area x Height

4. Let the base of a prism be a rectangle or square or triangle. If all of the side walls are triangles, then the prism will be a pyramid and it will look like as given below. 

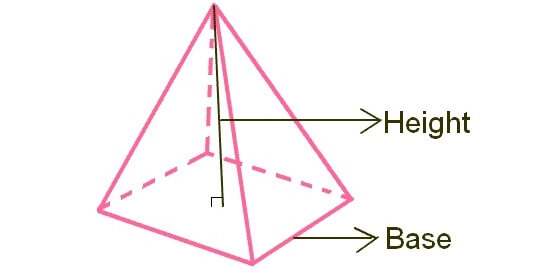
The formula to find volume of the above pyramid 

= (1/3) x Base Area x Height

Solved Problems

Problem 1 :

Find the volume of the cuboid given below.

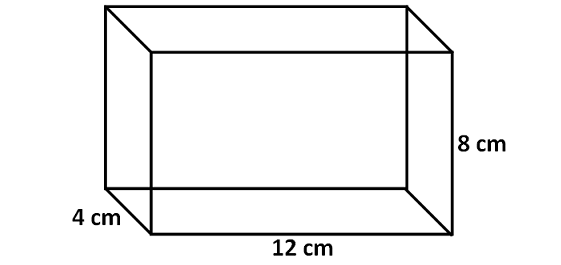
Solution :

Here, the base is  a rectangle and all the side walls are also rectangles.

Then, we have

Volume of the cuboid = Base Area x Height

Here, the base is a rectangle with length 12 cm and width 4 cm.

Area of base = 12 x 4 = 48 sq. cm

Height of the cuboid = 8 cm.

Volume of cuboid = 48 x 8

= 384 cubic cm

Problem 2 :

Find the volume of the cube given below.

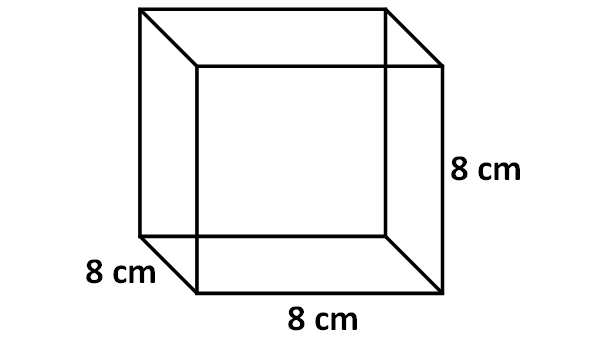
Solution :

Here, the base is  a square and all the side walls are also squares.

Then, we have

Volume of the cube = Base Area x Height

Here, the base is a square with side length of 8 cm.

Area of base = 8 x 8 = 64 sq. cm

Height of the cube = 8 cm.

Volume of cube = 64 x 8

= 512 cubic cm

Problem 3 :

Find the volume of the triangular prism given below.

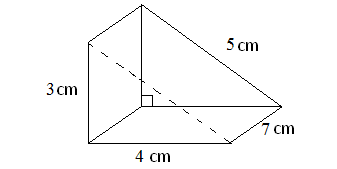
Solution :

Here, the base is  a rectangle, two of the side walls are triangles and other two side walls are rectangles.

Then, we have

Volume of the prism = (1/2) x Base Area x Height

Here, the base is a rectangle with length 7 cm and width is 4 cm.

So, area of the base = 7 x 4 = 28  sq. cm

Height of the prism = 3 cm

Volume of the prism = (1/2) x 28 x 3

= 42 cubic cm

Problem 4 :

Find the volume of the triangular prism given below.

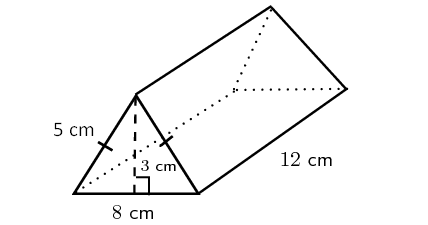
Solution :

Here, the base is  a rectangle, two of the side walls are triangles and other two side walls are rectangles.

Then, we have

Volume of the prism = (1/2) x Base area x Height

Here, the base is a rectangle with length 12 cm and width is 8 cm.

So, area of the base = 12 x 8 = 96 sq. cm

Height of the prism = 3 cm

Volume of the prism = (1/2) x 96 x 3

= 144 cubic cm

Problem 5 :

Find the volume of the triangular prism given below.

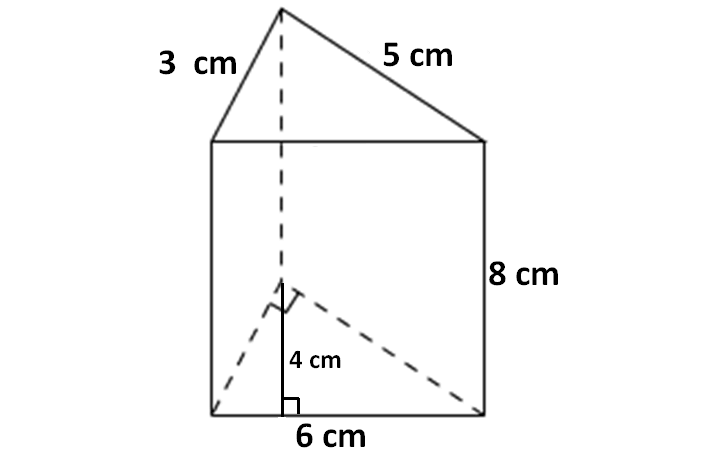
Solution :

Here, the base is  a triangle, and all the side walls are rectangles.

Then, we have

Volume of the prism = Base Area x Height

Here, the base is a triangle with base 6 cm and height 4 cm.

So, area of the base = (1/2) x 6 x 4 = 12 sq. cm.

Height of the prism = 8 cm.

Volume of the prism = 12 x 8

= 96 cubic cm

Problem 6 :

Find the volume of the pyramid given below.

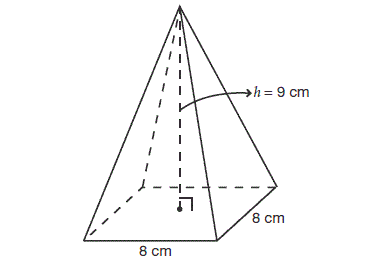
Solution :

Volume of the pyramid = (1/3) x Base Area x Height

Here, the base is a square with side length 8 cm.

So, area of the base = 8 x 8 = 64 sq. cm.

Height of the pyramid = 9 cm.

Volume of the pyramid = (1/3) x 64 x 9

= 192 cubic cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.