VOLUME OF 3D SHAPES WORKSHEET

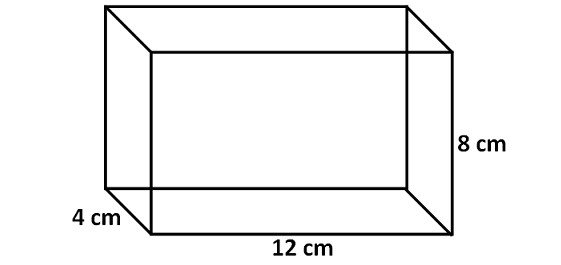
1)  Find the volume of the cuboid given below.

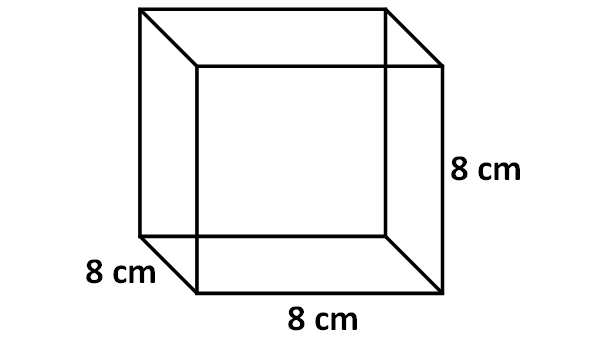
2)  Find the volume of the cube given below.

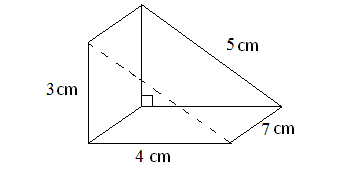
3)  Find the volume of the triangular prism given below.

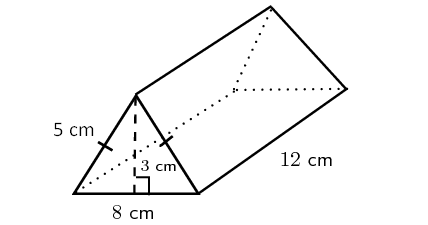
4)  Find the volume of the triangular prism given below.

5)  Find the volume of the triangular prism given below.

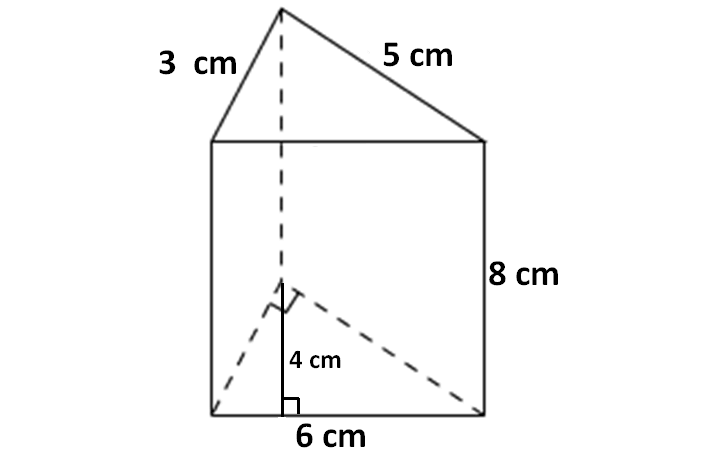
6)  Find the volume of the pyramid given below.

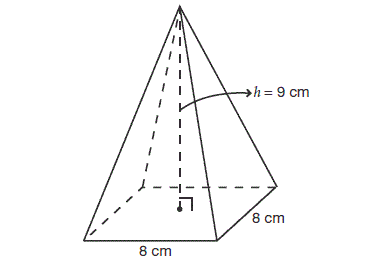
7)  Find the volume of the pyramid given below.

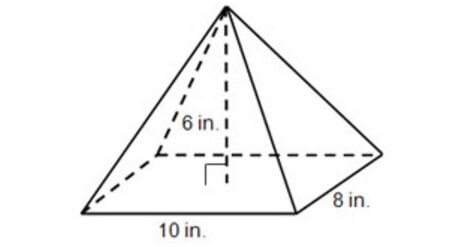
8)  Find the volume of the pyramid given below.

1. Answer :

Here, the base is  a rectangle and all the side walls are also rectangles.

Then, we have

Volume of the cuboid = Base Area x Height

Here, the base is a rectangle with length 12 cm and width 4 cm.

Area of base = 12 x 4 = 48 sq. cm

Height of the cuboid = 8 cm.

Volume of cuboid = 48 x 8

= 384 cubic cm

2. Answer :

Here, the base is  a square and all the side walls are also squares.

Then, we have

Volume of the cube = Base Area x Height

Here, the base is a square with side length of 8 cm.

Area of base = 8 x 8 = 64 sq. cm

Height of the cube = 8 cm.

Volume of cube = 64 x 8

= 512 cubic cm

3. Answer :

Here, the base is  a rectangle, two of the side walls are triangles and other two side walls are rectangles.

Then, we have

Volume of the prism = (1/2) x Base Area x Height

Here, the base is a rectangle with length 7 cm and width is 4 cm.

So, area of the base = 7 x 4 = 28  sq. cm

Height of the prism = 3 cm

Volume of the prism = (1/2) x 28 x 3

= 42 cubic cm

4. Answer :

Here, the base is  a rectangle, two of the side walls are triangles and other two side walls are rectangles.

Then, we have

Volume of the prism = (1/2) x Base area x Height

Here, the base is a rectangle with length 12 cm and width is 8 cm.

So, area of the base = 12 x 8 = 96 sq. cm

Height of the prism = 3 cm

Volume of the prism = (1/2) x 96 x 3

= 144 cubic cm

5. Answer :

Here, the base is  a triangle, and all the side walls are rectangles.

Then, we have

Volume of the prism = Base Area x Height

Here, the base is a triangle with base 6 cm and height 4 cm.

So, area of the base = (1/2) x 6 x 4 = 12 sq. cm.

Height of the prism = 8 cm.

Volume of the prism = 12 x 8

= 96 cubic cm

6. Answer :

Volume of the pyramid = (1/3) x Base Area x Height

Here, the base is a square with side length 8 cm.

So, area of the base = 8 x 8 = 64 sq. cm.

Height of the pyramid = 9 cm.

Volume of the pyramid = (1/3) x 64 x 9

= 192 cubic cm

7. Answer :

Volume of the pyramid = (1/3) x Base area x Height

Here, the base is a rectangle with side length 10 inches and width 8 inches.

So, area of the base = 10 x 8 = 80 sq. inches.

Height of the pyramid = 6 inches.

Volume of the pyramid = (1/3) x 80 x 6

= 160 cubic inches

8. Answer :

Volume of the pyramid = (1/3) x Base area x Height

Here, the base is a triangle with height 7 inches and base 8 inches.

So, area of the base = (1/2) x 8 x 7 = 28 sq. inches.

Height of the pyramid = 9 inches.

Volume of the pyramid = 28 x 9

= 252 cubic inches

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.