VOLUME OF 3D SHAPES QUESTIONS WITH ANSWERS

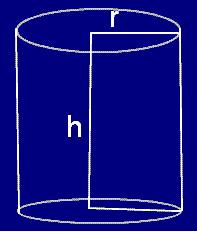
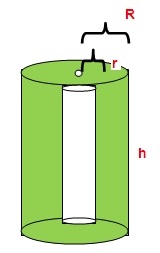
Volume  =  Πr2h	Volume  =  Πh(R2 - r2)
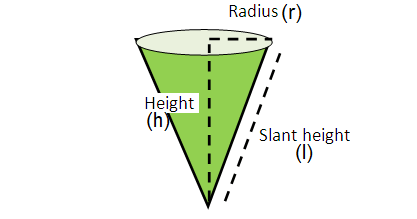
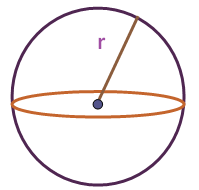
Volume  =  (1/3) Πr2h	Volume  =  (4/3) Πr3 Volume of hollow sphere   =  (4/3) Π(R3 - r3)
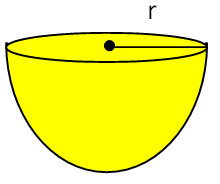
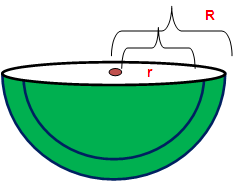
Volume  =  (2/3) Πr3	Volume = (2/3)Π(R3 - r3)
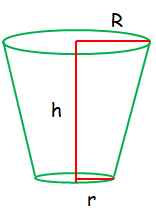	Volume = (1/3)Πh(R2 + r2 + Rr)

Example 1 :

A right angled triangle whose sides are 6 cm, 8 cm and 10 cm is revolved about the sides containing the right angle in two ways. Find the difference in volumes of the two solids so formed.

Solution :

The longest side of a triangle is 10 cm

If the triangle is revolved about 6 cm

r = 6 cm and h = 8 cm

Volume of solid, when it is revolved about 6 cm,

  =  (1/3)πr²h

  =  (1/3)π 6² (8)

  =  96π cm³

Volume of solid, when it is revolved about 8 cm,

r = 8 cm and h = 6 cm

  =  (1/3)πr²h

  =  π 8² (6)

  =  128π cm³

Difference  =  128π - 96π

  =  32π cm³

  =  32(22/7)

=  100.5 cm³

Example 2 :

The volumes of two cones of same base radius are 3600 cm³ and 5040 cm³. Find the ratio of heights.

Solution :

Let "h₁" and "h₂" be the heights of 1^st and 2^nd cone.

Volume of 1^st cone  =  3600 cm³

 (1/3)πr²h₁  =  3600 cm³

Volume of 2^nd cone  =  5040 cm³

 (1/3)πr²h₂  =  5040 cm³

h₁ : h₂  =  3600 : 5040

h₁ / h₂  =  3600 / 5040

h₁ : h₂  =  5 : 7

Example 3 :

If the ratio of radii of two spheres is 4 : 7, find the ratio of their volumes.

Solution :

Radius of 1^st sphere (r₁) =  4x

Radius of 2^nd sphere  (r₂)  =  7x

Volume of sphere  =  (4/3) πr³

(4/3) πr₁³ : (4/3) πr₁³

(4x)³ : (7x)³

64 : 343

Example 4 :

A solid sphere and a solid hemisphere have equal total surface area. Prove that the ratio of their volume is 3 √3 : 4 .

Solution :

Total surface area of sphere = 4πr₁²

Total surface area of hemisphere = 3πr₂²

4πr₁²= 3πr₂²

r₁²= (3/4)r₂²

r₁  = (√3/2)r₂

Volume of sphere  =  (4/3) πr₁³

Volume of hemisphere  =  (2/3) πr₁³

  (4/3) πr₁^{3 :} (2/3) πr₂³

  2((√3/2))^{3 :} r₂³

  2(3√3/8)  r₂³: r₂³

  3√3 : 4

Hence it is proved.

Example 5 :

The outer and the inner surface areas of a spherical copper shell are 576π cm² and 324π cm² respectively. Find the volume of the material required to make the shell.

Solution :

Outer curved surface area of sphere  =  4πR²

Inner curved surface area of sphere  =  4πr²

4πR²  =  576π

R²  =  576/4  =  144

R  =  12

4πr²  =  324π

r²  =  324/4  =  81

r  =  9

Volume of sphere  =  (4/3) π (R³ - r³)

  =  (4/3) π (12³ - 9³)

  =  (4/3) π (1728 - 729)

  =  (4/3) π (999)

=  1332(22/7)

=  4186.28 cm³

Example 6 :

A container open at the top is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends are 8 cm and 20 cm respectively. Find the cost of milk which can completely fill a container at the rate of ₹40 per liter.

Solution :

Volume of milk in the frustum container 

  = (1/3)Πh(R² + r² + Rr)

h = 16 cm, r = 8 cm, R = 20 cm

  = (1/3)Π (16)(20² + 8² + 20(8)) - Πr²

  =  (22/7) [(1/3)(16)(20² + 8² + 20(8)) - 64]

  =  (22/7) [(1/3)(16)(624) - 64]

  =  (22/7) [3264]

  =  10258.28 cm³

1000 cm³  =  1 liter

  =  10.25828 liter

Cost per liter  =  ₹40

  =  40(10.258)

  =  ₹410.32

Example 7 :

If each side of a cube is increased by 10%. What is the percentage increase in surface area of the cube ?

Solution :

Side length of the cube = x

Side length is increased by 10%. Then new side length = 110% of x

= 1.10x

Surface area of cube = 6a²

= 6(1.10x)²

= 6(1.21x²)

= 7.26x²

Percentage increase or decrease

= { |old value - new value| / old value } x 100%

= {|7.26x² - 6x²| / 6x²} x 100%

= {1.26x²/6x²} x 100%

= 0.21x² x 100%

= 21%

Example 8 :

The internal and external diameters of hollow hemispherical vessel are 24 cm and 25 cm respectively. If the cost of painting 1cm² surface area is $1.5, find the total cost of painting the vessel all over.

Solution :

Internal diameter = 24 cm

radius (r) = 12 cm

External diameter = 25 cm

Radius (R) = 25/2

Surface area of hemisphere = 2Π(R² - r²)

= 2 x (22/7) x ((25/2)² - 12²)

= 2 x (22/7) x ((625 - 576)/4)

= 2 x (22/7) x (49/4)

= 77 cm²

Total cost of painting = 1.5 x 77

= $115.5

Example 9 :

The surface area of a sphere of radius 5 cm is five times the area of the curved surface area of a cone of radius 4cm. Find the height of the cone

Solution :

Surface area of sphere = 5(surface area of cone)

4πr² =  5(πrl)

radius of sphere = 5 cm

radius of cone = 4 cm

height of cone = h

l = ?

4π(5)² =  5(π(4)l)

100 / 20 = l

l = 5 cm

l² = h² + r²

5² = 4² + h²

h² = 25 - 16

h = 3 cm

So, height of the cone is 3 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.