HOW TO CHECK IF GIVEN FOUR POINTS FORM A SQUARE

How to Check if Given Four Points Form a Square ? 

Here we are going to see how to check if the given four points form a square.

We have to follow the steps given below in order to check if given four points form a square.

(i)  Plot the given points in the graph and join the points.

(ii)  Find the length of all sides.

(iii)  In a square length of all sides will be equal.

(iv)  The diagonals will have same length.

If the given points satisfies the conditions (iii) and (iv), we may decide that the points form a square.

Let us see some example problems.

Example :

Examine whether the given points 

A (2, 6), B (5, 1), C (0, -2) and D (-3, 3)

forms a square.

Solution :

Step 1 :

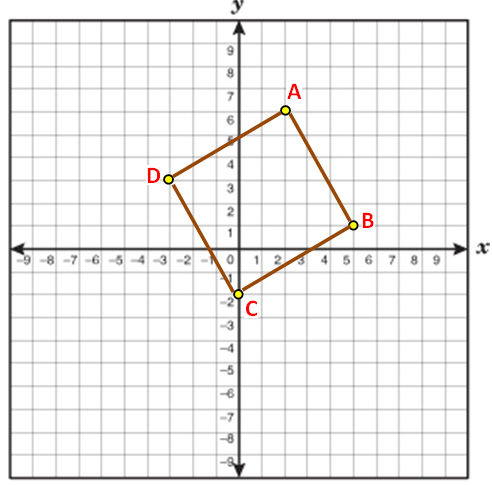
Step 2 :

Finding the length of all sides.

Distance Between Two Points (x₁, y₁) and (x₂, y₂)

√(x₂ - x₁)² + (y₂ - y₁)²

Four points are A (2,6) and B (5,1) and C (0,-2) and D (-3,3)

Length of AB :

Here x₁ = 2, y₁ = 6, x₂ = 5  and  y₂ = 1

=  √(5-2)² + (1-6)²

=  √3²+(-5)²

=  √9+25

=  √34 units  ----(1)

Length of BC :

Here x₁ = 5, y₁ = 1, x₂ = 0  and  y₂ = -2

=  √(0-5)² + (-2-1)²

=  √(-5)² + (-3)2

=  √(25 + 9)

=  √34 units  ----(2)

Length of CD :

Here x₁ = 0, y₁ = -2, x₂ = -3  and  y₂ = 3

=  √(-3-0)² + (3-(-2))²

=  √(-3)² + (3+2)²

=  √9 + 25

=  √34 units  ----(3)

length of DA :

Here x₁ = -3, y₁ = 3, x₂ = 2  and  y₂ = 6

=  √(2-(-3))² + (6-3)²

=  √5² + 3²

=  √25 + 9

=  √34 units  ----(4)

Step 3 :

Length of diagonal AC :

Here x₁ = 2, y₁ = 6, x₂ = 0 and  y₂ = -2

=  √(0-2)² + (-2-6)²

=  √(-2)² + (-8)²

=   √4 + 64

=  √70 units

Length of diagonal BD :

Here x₁ = 5, y₁ = 1, x₂ = -3 and  y₂ = 3

=  √(-3-5)² + (3-1)²

=  √(-8)² + (2)²

=  √64 + 4

=  √70 units

Length of diagonal AC  =  Length of diagonal BD

So, the given points are vertices of square.

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.