VERTICAL STRETCH AND COMPRESSION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
How to Do Vertical Stretch in a Function
Let f(x) be a function.
Let g(x) be a function which represents f(x) after a vertical stretch by a factor of k.
where, k > 1.
In the function f(x), to do vertical stretch by a factor of k, at every where of the function, y co-ordinate has to be multiplied by k.
The graph of g(x) can be obtained by stretching the graph of f(x) vertically by the factor k.
Note :
Point on the original curve : (x, y)
Point on the curve after it is vertically stretched by the factor of k :
(x, ky)
How to Do Vertical Compression in a Function
Let f(x) be a function.
Let g(x) be a function which represents f(x) after a vertical compression by a factor of k.
where k > 1.
In the function f(x), to do vertical compression by a factor of k, at every where of the function, y co-ordinate has to be multiplied by 1/k.
The graph of g(x) can be obtained by compressing the graph of f(x) vertically by the factor k.
Note :
Point on the original curve : (x, y)
Point on the curve after it is vertically compressed by the factor of k :
(x, (1/k)y)
Example 1 :
Perform a vertical stretch by a factor 2 to the function
f(x) = x2
And
also write the formula that gives the requested transformation and draw
the graph of both the given function and the transformed function
Answer :
Step 1 :
Let g(x) be a function which represents f(x) after the vertical stretch by a factor of 2.
Since we do vertical stretch by the factor 2, we have to replace x2 by 2x2 in f(x) to get g(x).
Step 2 :
So, the formula that gives the requested transformation is
g(x) = 2x2
Step 3 :
The graph g(x) = 2x2 can be obtained by stretching the graph of the function f(x) = x2 vertically by the factor 2.
(x, y) -----> (x, 2y)
Step 4 :
Table of values :
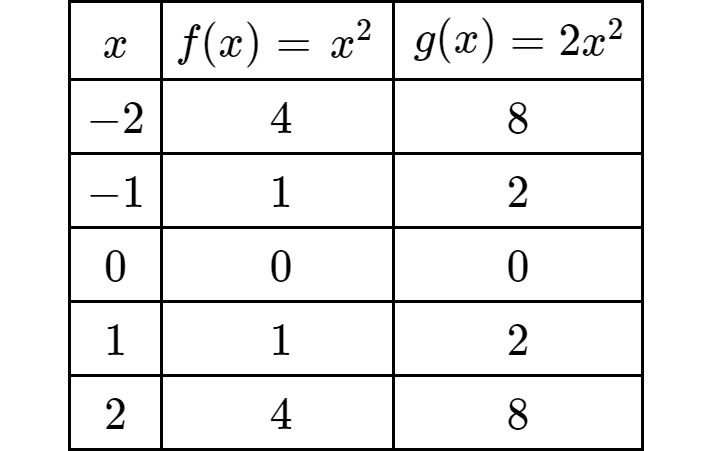
Step 5 :
Graphs of f(x) and g(x) :
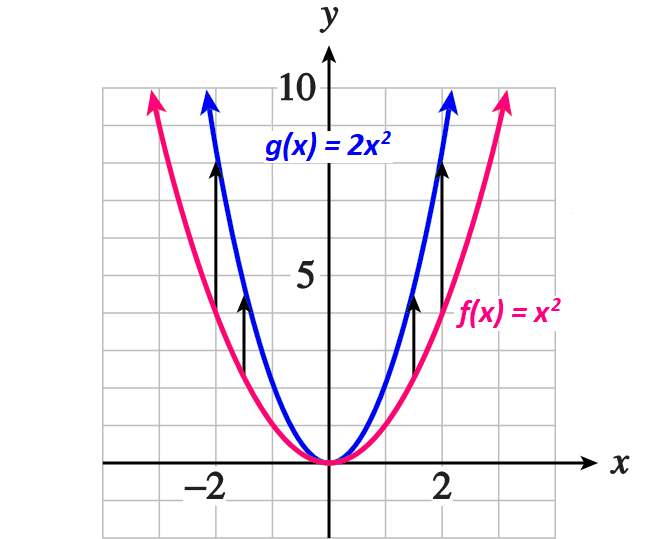
Example 2 :
Perform a vertical compression by a factor 2 to the function
f(x) = x2
And also write the formula that gives the requested transformation and draw the graph of both the given function and the transformed function
Answer :
Step 1 :
Let g(x) be a function which represents f(x) after the vertical compression by a factor of 2.
Since we do vertical compression by the factor 2, we have to replace x2 by (1/2)x2 in f(x) to get g(x).
Step 2 :
So, the formula that gives the requested transformation is
g(x) = (1/2)x2
Step 3 :
The graph g(x) = (1/2)x2 can be obtained by compressing the graph of the function f(x) = x2 vertically by the factor 2.
(x, y) -----> (x, (1/2)y)
Step 4 :
Table of values :
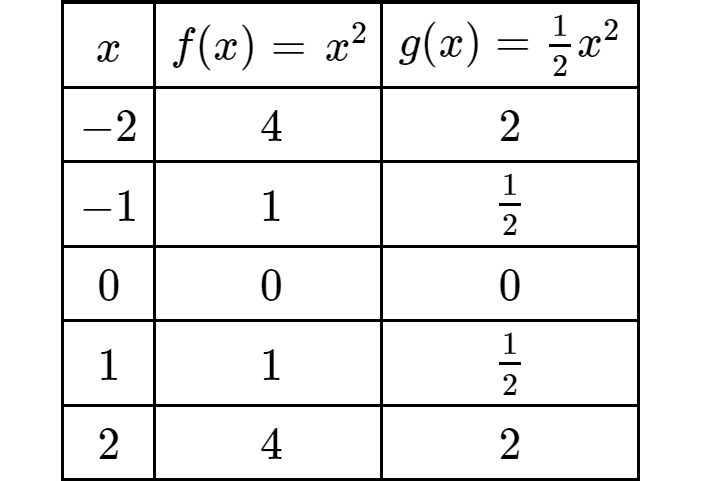
Step 5 :
Graphs of f(x) and g(x) :
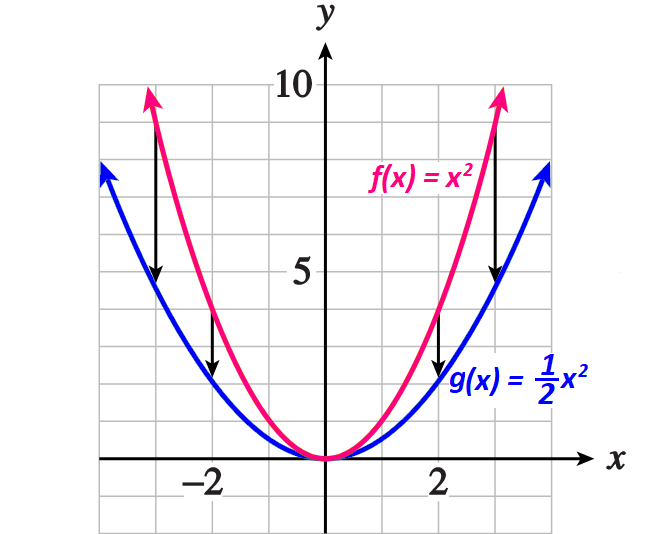
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

