VERTICAL ANGLES THEOREM

Vertical Angles meet at a vertex but are on opposite sides of the intersecting lines (definition). 

Theorem – If two lines intersect then vertical angles are congruent

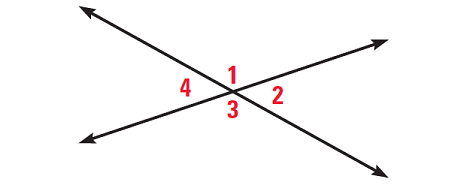
In the above diagram, vertical angles are

Angle 1 and angle 3

Angle 2 and angle 4

So, 

m∠1 ≅ m∠3 ----> m∠1 = m∠3

m∠2 ≅ m∠4 ----> m∠2 = m∠4

Example 1 :

Look at the picture shown below and answer the following questions. 

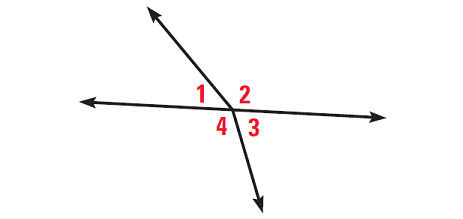
(i)  Are ∠1 and ∠3 vertical angles ?

(ii)  Are ∠2 and ∠4 vertical angles ?

Solution : 

Solution (i) : 

No. The angles are adjacent but their non-common sides are not opposite rays.

Solution (ii) : 

Yes. The angles are adjacent and their non-common sides are opposite rays.

Solution (iii) : 

No. The sides of the angles do not form two pairs of opposite rays.

Solution (iv) : 

No. The sides of the angles do not form two pairs of opposite rays.

Example 2 :

In the diagram shown below, using Linear Pair Postulate, solve for x and y. Then, find the angle measures and analyze your results with Vertical Angles Theorem. 

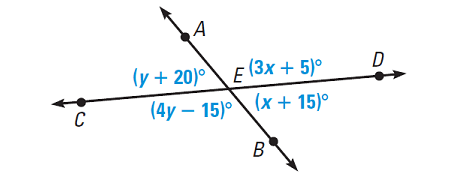
Solution : 

Use the fact that the sum of the measures of angles that form a linear pair is 180°. 

Solving for x :

∠AED and ∠DEB form a linear pair.

m∠AED + m∠DEB  =  180°

Substitute m∠AED = (3x + 5)° and m∠DEB = (x + 15)°.

(3x + 5)° + (x + 15)°  =  180°

Simplify.

4x + 20  =  180

Subtract 20 from each side.  

4x  =  160

Divide each side by 4.

x  =  40

Solving for y :

∠AEC and ∠CEB form a linear pair. 

m∠AEC + m∠CEB  =  180°

Substitute m∠AEC = (y + 20)° and m∠CEB = (4y - 15)°.

(y + 20)° + (4y - 15)°  =  180°

Simplify.

5y + 5  =  180

Subtract 5 from each side.  

5y  =  175

Divide each side by 5.

y  =  35

Use substitution to find the angle measures :

m∠AED  =  (3x + 5)°  =  (3 • 40 + 5)°  =  125°

m∠DEB  =  (x + 15)°  =  (40 + 15)°  =  55°

m∠AEC  =  ( y + 20)°  =  (35 + 20)°  =  55°

m∠CEB  =  (4y - 15)°  =  (4 • 35 - 15)°  =  125°

So, the angle measures are 125°, 55°, 55°, and 125°. Because the vertical angles are congruent, the result is reasonable.

Example 3 :

In the stair railing shown at the right,if∠6 has a measure of 130°, find the measures of the other three angles.

Solution : 

∠6 and ∠8 are vertical angles, they are equal.  

m∠8  =  m∠6

Substitute m∠6 = 130°. 

m∠8  =  130°

∠5 and ∠6 form a linear pair, they are supplementary. 

m∠5 + m∠6  =  180°

Substitute m∠6 = 130°.

m∠5 + 130°  =   180°

Subtract 130° from both sides.

m∠5  =   50°

∠5 and ∠7 are vertical angles, they are equal.  

m∠7  =  m∠5

Substitute m∠5 = 50°. 

m∠7  =  50°

Therefore, 

m∠5  =  50°

m∠7  =  50°

m∠8  =  130°

Example 4 :

Determine the missing angle measures and explain how you are arrived the answer.

Solution :

30 and x are vertically opposite angles, then they are equal.

z and y are vertically opposite angles and 30 and y are adjacent angles.

30 + y = 180

y = 180 - 30

y = 150

Example 5 :

Given the diagram below, determine the missing angles:

(a) m∠𝐶𝑋𝐹 = 

(b) m∠𝐵𝑋𝐴 =

(c) m∠𝐴𝑋𝐺 =

(d) m∠𝐺𝑋𝐸 =

(e) m∠𝐸𝑋𝐷 =

Solution :

(a)

m∠𝐶𝑋𝐹 = m∠𝐶XD - m∠FXD

= 90 - 40

m∠𝐶𝑋𝐹 = 50

(b)

m∠𝐵𝑋𝐴 = m∠𝐶XA - m∠CXB

= 90 - 32

= 58

(c)

m∠𝐴𝑋𝐺 = m∠FXD

Vertically opposite angles will be equal.

m∠𝐴𝑋𝐺 = 40

(d)

m∠𝐺𝑋𝐸 = m∠EXA - m∠𝐺𝑋A

= 90 - 40

= 50 (also m∠𝐶𝑋𝐹 is vertically opposite angles)

(e)

m∠𝐸𝑋𝐷 = 90 (m∠AXC is vertically opposite angles)

Example 6 :

Determine the number that represents x, y, or z in each diagram below. 

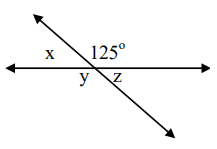
Solution :

Vertically opposite angels are equal. Then y = 125

x + 125 = 180

x = 180 - 125

x = 55

z = 55

So, the values of x, y and z are 55, 125 and 55 respectively.

Example 7 :

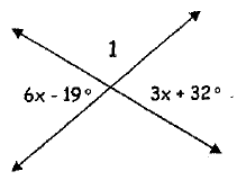
Solution :

Vertically opposite angles will be equal.

6x - 19 = 3x + 32

6x - 3x = 32 + 19

3x = 51

x = 51/3

x = 17

Example 8 :

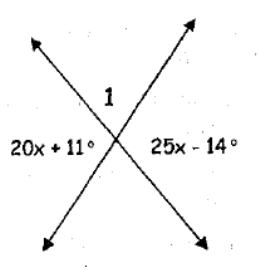
Solution :

Vertically opposite angles will be equal.

20x + 11 = 25x - 14

20x - 25x = -14 - 11

-5x = -25

x = 25/5

x = 5

Example 9 :

Solution :

<2 = 33 (vertically opposite angles)

<2 + 59 + <1 = 180

33 + 59 + <1 = 180

92 + <1 = 180

<1 = 180 - 92

<1 = 88

<3 = 88

<4 = 59

Example 10 :

Solution :

<2 = 37 (vertically opposite angles)

90 + <1 + <2 = 180

90 + <1 + 37 = 180

<1 + 127 = 180

<1 = 180 - 127

<1 = 53

<3 = 90 + <1

<3 = 90 + 53

<3 = 143

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.