VERTEX FORM OF A QUADRATIC EQUATION

Learning Objectives :

* Vertex form of a quadratic equation.

* If a quadratic equation is given in standard form, how to write it in vertex form.

* How to sketch the graph of a quadratic equation that is in vertex form.

Vertex form of a quadratic equation :

y = a(x - h)² + k

where (h, k) is the vertex of the parabola. 

The h represents the horizontal shift and k represents the vertical shift. 

Horizontal Shift :

Shifting the graph of the parent function y = x² to the left or right from x = 0. 

Vertical Shift :

Shifting the graph of the parent function y = x² up or down from x = 0. 

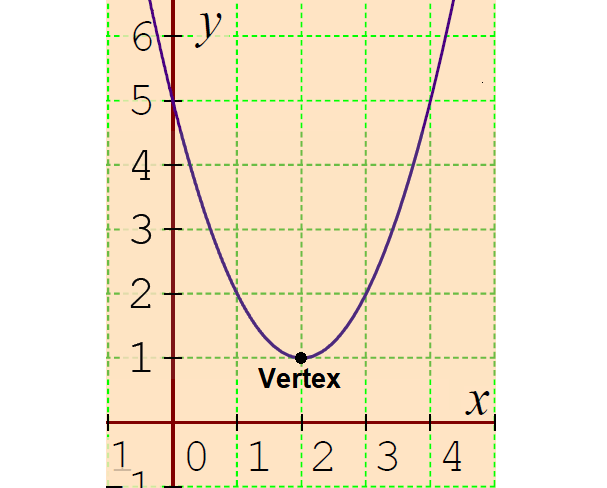
In the above picture, the graph (Parabola) of the parent function y = x² is shifted 2 units to the right from x = 0 and 1 unit up from y = 0. 

So, the vertex is

(Horizontal shift, Vertical shift) = (2, 1)

Example 1 :

Write the quadratic equation in vertex form and write its vertex : 

y = -x² - 2x - 2

Solution :

Vertex form of the quadratic equation :

y = -x² - 2x - 2

y = -(x² + 2x) - 2

y = -[x² + 2(x)(1) + 1² - 1²] - 2

y = -[(x + 1)² - 1²] - 2

y = -[(x + 1)² - 1] - 2

y = -(x + 1)² + 1 - 2

y = -(x + 1)² - 1

Vertex :

Comparing y = a(x - h)² + k and y = -(x + 1)² - 1,

h = -1 and k = -1

So, the vertex is (h, k) = (-1, -1).

Example 2 :

Write the quadratic equation in vertex form and sketch the graph. 

y = -x² + 2x + 3

Solution :

Vertex form of the quadratic equation :

y = -x² + 2x + 3

y = -(x² - 2x) + 3

y = -[x² - 2(x)(1) + 1² - 1²] + 3

y = -[(x - 1)² - 1²] + 3

y = -[(x - 1)² - 1] + 3

y = -(x - 1)² + 1 + 3

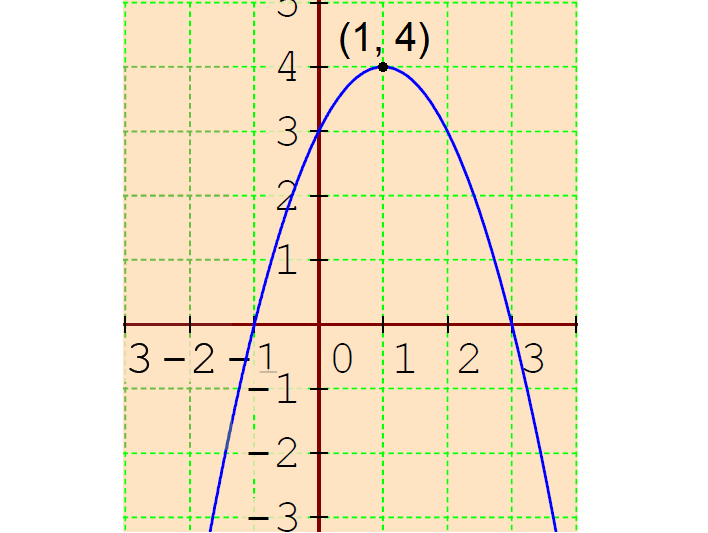
y = -(x - 1)² + 4

Vertex :

Comparing y = a(x - h)² + k and y = -(x - 1)² + 4,

h = 1 and k = 4

So, the vertex is (h, k) = (1, 4).

To graph the above quadratic equation, we need to find x-intercept and y-intercept, if any.

x-intercept :

To find the x-intercept, substitute y = 0. 

0 = -(x - 1)² + 4

(x - 1)² = 4

Take square root on both sides.

x - 1 = ±√4

x - 1 = ±2

x - 1 = -2  or  x - 1 = 2

x = -1  or  x = 3

So, the x-intercepts are (-1, 0) and (3, 0) .

y-intercept :

To find the y-intercept, substitute x = 0.

y = -(0 - 1)² + 4

y = -(-1)² + 4

y = -1 + 4

y = 3

So, the y-intercept is (0, 3).

Comparing y = a(x - h)² + k and y = -(x - 1)² + 4,

a = -1

So, the parabola opens down with vertex (1, 4), x-intercepts (-1, 0) and (3, 0) and y-intercept (0, 3).

Example 3 :

Given f(x) = x² + 2x - 2, find the following.

a) y-intercept     b) Axis of symmetry

c)  The coordinate of the vertex

d)  Idnetify the vertex as a maximum or minimum.

Solution :

f(x) = x² + 2x - 2

a)  y-intercept :

Put x = 0

f(x) = y

y = 0² + 2(0) - 2

y = -2

b) Axis of symmetry

Equation of axis of symmetery x = -b/2a

a = 1, b = 2 and c = -2

x = -2/2(1)

x = -1

c)  The coordinate of the vertex

f(x) = x² + 2x(1) + 1²- 1² - 2

= (x + 1)² - 1 - 2

f(x) = (x + 1)² - 3

Comparing with y = (x - h)² + k

we get (h, k) ==>  (-1, -3). So the vertex is at (-1, -3)

d)  Identify the vertex as a maximum or minimum.

Since the parabola opens up, it may have minimum at x = -1 and the minimum value is -3.

Example 4 :

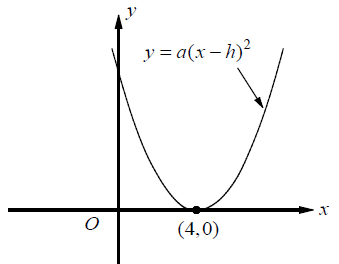
In the xy-plane above, the parabola y = a(x - h)² has one x-intercept at (4, 0). If the y-intercept of the parabola is 9, what is the value of a ?

Solution :

Applying the vertex in the equation above,

y = a(x - 4)²

y-intercept of the parabola is 9, then we know that the parabola will pass through the point (0, 9).

9 = a(0 - 4)²

9 = a(- 4)²

9 = 16a

a = 9/16

So, the value of a is 9/16.

Example 5 :

In the xy-plane, if the parabola with equation

y = a(x + 2)² - 15

passes through (1, 3), what is the value of a ?

Since the parabola passes through the point (1, 3), we apply x = 1 abd y = 3 in the equation above.

3 = a(1 + 2)² - 15

3 + 15 = a(3)²

18 = 9a

a = 18/9

a = 2

So, the value of a is 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.