VENN DIAGRAM WORD PROBLEMS WITH 3 CIRCLES

Let us consider the three sets A, B and C.

Set A contains a elements, B contains b elements and C contains c elements.

Both A and B contains w elements, B and C contains x elements, A and C contains y elements, all the three sets A, B and C contains z elements.

We can use Venn diagram with 3 circles to represent the above information as shown below. 

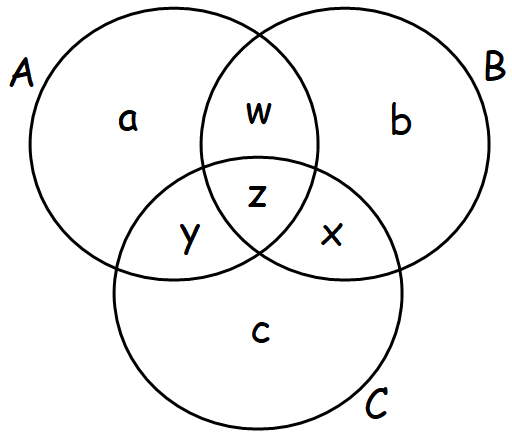
Let us do the following changes in the Venn diagram. 

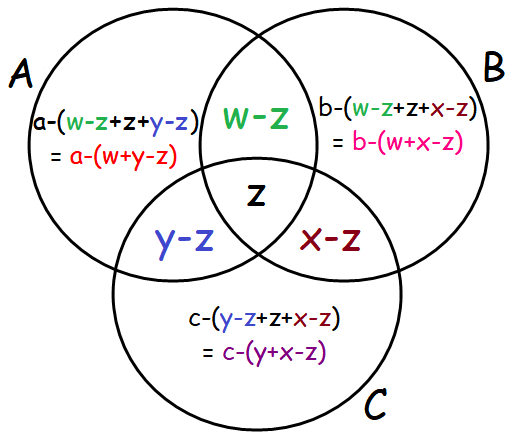
We can get the following results from the Venn diagram shown above.

Number of elements related only to A is 

=  a - (w + y - z)

Number of elements related only to B is 

=  b - (w + x - z)

Number of elements related only to C is 

=  c - (y + x - z)

Number of elements related only to (A and B) is

=  w - z

Number of elements related only to (B and C) is

=  x - z

Number of elements related only to (A and C) is

=  y - z

Number of elements related to all the three sets A, B and C is 

=  z

Total number of elements related to all the three sets A, B and C  is

= [a-(w+y-z)] + [b-(w+x-z)] + [c-(y+x-z)] + (w-z) + (x-z) + (y-z) + z 

Example 1 :

In a survey of university students, 64 had taken mathematics course, 94 had taken chemistry course, 58 had taken physics course, 28 had taken mathematics and physics, 26 had taken mathematics and chemistry, 22 had taken chemistry and physics course, and 14 had taken all the three courses. Find how many had taken one course only.

Solution :

Step 1 :

Let M, C and P represent the courses Mathematics, Chemistry and Physics respectively.

Venn diagram related to the information given in the question: 

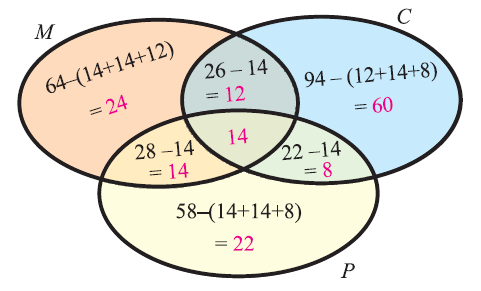
Step 2 :

From the venn diagram above, we have

No. of students who had taken only math  =  24

No. of students who had taken only chemistry  =  60

No. of students who had taken only physics  =  22

Step 3 :

Total no. of students who had taken only one course :

=  24 + 60 + 22

=  106

So, the total number of students who had taken only one course is 106.

Example 2 :

In a group of students, 65 play foot ball, 45 play hockey, 42 play cricket, 20 play foot ball and hockey, 25 play foot ball and cricket, 15 play hockey and cricket and 8 play all the three games. Find the total number of students in the group (Assume that each student in the group plays at least one game.)

Solution :

Step 1 :

Let F, H and C represent the games football, hockey and cricket respectively. 

Venn diagram related to the information given in the question :

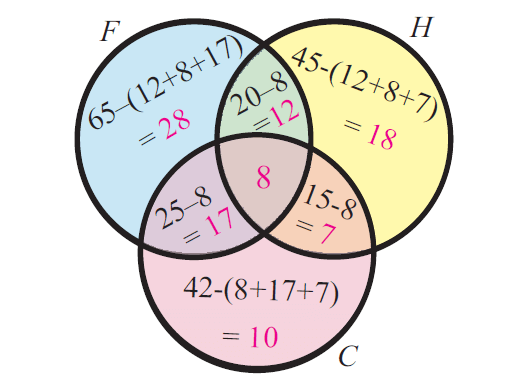
Step 2 :

Total number of students in the group :

=  28 + 12 + 18 + 7 + 10 + 17 + 8

=  100

So, the total number of students in the group is 100.

Example 3 :

In a college, 60 students enrolled in chemistry,40 in physics, 30 in biology, 15 in chemistry and physics,10 in physics and biology, 5 in biology and chemistry. No one enrolled in all the three. Find how many are enrolled in at least one of the subjects.

Solution :

Let C, P and B represent the subjects Chemistry, Physics and Biology respectively.

Venn diagram related to the information given in the question :

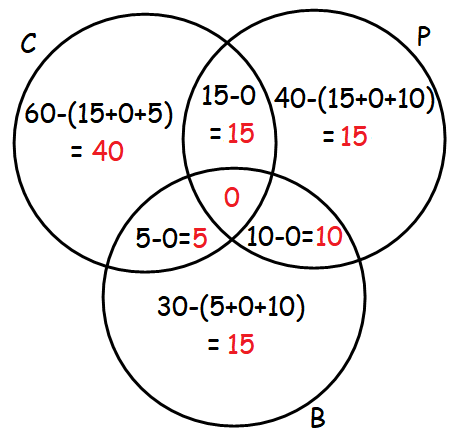
From the above Venn diagram, number of students enrolled in at least one of the subjects :

=  40 + 15 + 15 + 15 + 5 + 10 + 0

=  100

So, the number of students enrolled in at least one of the subjects is 100.

Example 4 :

In a town 85% of the people speak Tamil, 40% speak English and 20% speak Hindi. Also 32% speak Tamil and English, 13% speak Tamil and Hindi and 10% speak English and Hindi, find the percentage of people who can speak all the three languages.

Solution :

Let T, E and H represent the people who speak the languages Tamil, English and Hindi respectively. 

Let x be the percentage of people who speak all the three languages.

Venn diagram related to the information given in the question :

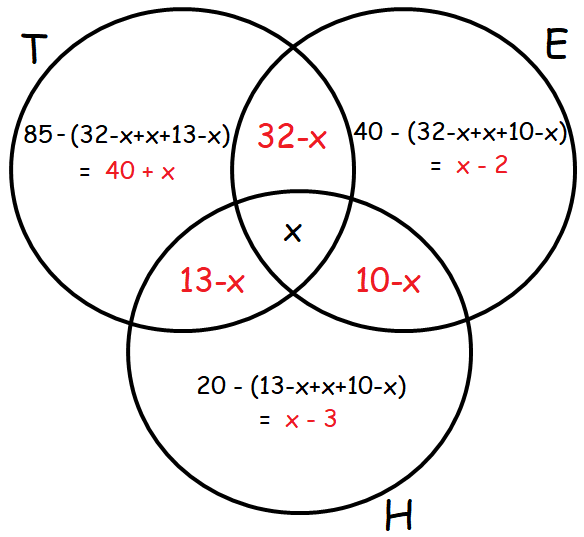
From the above Venn diagram, we can have 

100  =  40 + x + 32 – x + x + 13 – x + 10 – x – 2 + x – 3 + x

100  =  40 + 32 + 13 + 10 – 2 – 3 + x 

100  =  95 – 5 + x

100  =  90 + x

x  =  100 - 90

x  =  10% 

So, the percentage of people who speak all the three languages is 10%. 

Example 5 :

An advertising agency finds that, of its 170 clients, 115 use Television, 110 use Radio and 130 use Magazines. Also 85 use Television and Magazines, 75 use Television and Radio, 95 use Radio and Magazines, 70 use all the three. Draw Venn diagram to represent these data. Find 

(i) how many use only Radio?

(ii) how many use only Television?

(iii) how many use Television and Magazine but not radio?

Solution :

Let T, R and M represent the people who use Television, Radio and Magazines respectively.

Venn diagram related to the information given in the question :

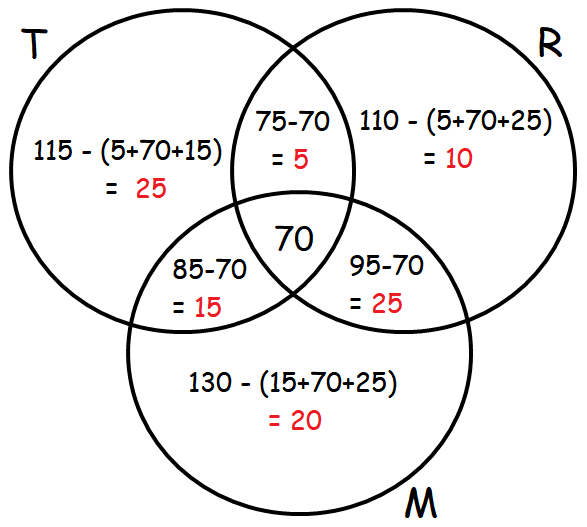
From the above Venn diagram, we have

(i) Number of people who use only Radio is 10

(ii) Number of people who use only Television is 25

(iii) Number of people who use Television and Magazine but not radio is 15.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.