VENN DIAGRAM WORD PROBLEMS WITH 2 CIRCLES

Example 1 :

In a class of 50 students, each of the students passed either in mathematics or in science or in both. 10 students passed in both and 28 passed in science. Find how many students passed in mathematics?

Solution :

Let M = The set of students passed in Mathematics

S = The set of students passed in Science

We may solve the given problem using two methods.

(i) Using formula

(ii) Using venn diagram

Method 1 : 

Total number of students  n (M U S)  =  50

Number of students passed in both subjects n(MnS) = 10

Number of students passed in science n (S)  =  28

From this, we have to find the number of students who passed in mathematics.

n (M U S)  = n (M) + n (S) -  n (M n S)

50  =  n (M) + 28 - 10

50  =  n (M) + 18

Subtract 18 on both sides

50 - 18 = n (M) + 18 - 18

n (M) = 32

So, the number students passed in Mathematics is 32.

Method 2 :

Let "x" be the number of students passed in Mathematics.

By representing the given details in venn diagram, we get

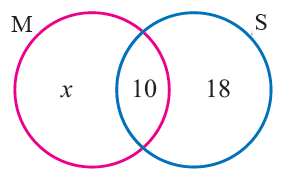
From the Venn diagram

x + 10 + 18 = 50

x = 50 - 28 = 22

Number of students passed in Mathematics

= x + 10

= 22 + 10

= 32

Example 2 :

The population of a town is 10000. Out of these 5400 persons read newspaper A and 4700 read newspaper B. 1500 persons read both the newspapers. Find the number of persons who do not read either   of the two papers.

Solution :

Let A = The set of persons who read newspaper A

B = The set of persons who read newspaper B

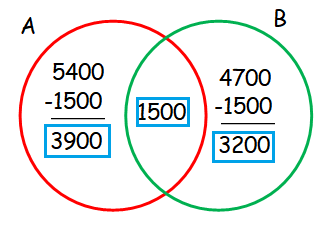
Number of persons who read at least one news paper

= 3900 + 1500 + 3200

=  8600

Total population  =  10000

To find the number of persons who do not read either   of the two papers, we have to subtract number of persons who read at least one from total population.

  =  10000 - 8600

  =  1400

So, the number of persons who do not read either   of the two papers is 1400.

Example 3 :

In a school, all the students play either Foot ball or Volley ball or both. 300 students play Foot ball, 270 students play Volley ball and 120 students play both games. Find

(i) the number of students who play Foot ball only

(ii) the number of students who play Volley ball only

(iii) the total number of students in the school

Solution :

Let A = The set of students who play foot ball 

B = The set of students who play volley ball

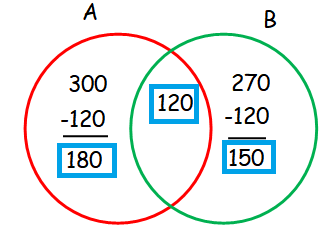
(i) The number of students who play Foot ball only is 180

(ii)The number of students who play Volley ball only is 150

(iii) The total number of students in the school

  =  180 + 120 + 150

  =  450

Example 4 :

In a School 150 students passed X Standard Examination. 95 students applied for Group I and 82 students applied for Group II in the Higher Secondary course. If 20 students applied neither of the two, how many students applied for both groups?

Solution :

A = The set of students who applied for Group I

B = The set of students who applied for Group II

Number of students who applied at least one group

  =  150 - 20

  =  130

n (A) = 95, n (B) = 82 and n (A U B) = 130

n (A U B) = n (A) + n (B) - n (A n B)

130 =  95 + 82 - n (A n B)

130  =  177 - n (A n B)

 n (A n B)  =  177 - 130  ==> 47

So, the number of students applied for both groups is 47.

Example 5 :

If the Venn diagram alongside illustrates the number of people in a sporting club who play tennis (T) and hockey (H), determine the number of people:

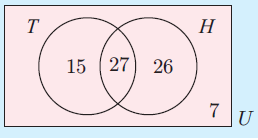
a) in the club

b) who play hockey

c) who play both sports

d) who play neither sport

e) who play at least one sport.

Solution :

a) Number of people in the club = 15 + 27 + 26 + 7

= 75

b)  Number of people who play hockey = 27 + 26

= 53

c)  Number of people who play both sports = 27

d)  Number of people who play neither sport = 7

e) Number of people who play at least one sport 

= 15 + 27 + 26

= 68

Example 6 :

The Venn diagram alongside illustrates the number of students in a particular class who study Chemistry (C) and History (H). Determine the number of students:

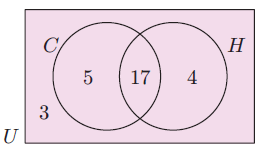
a) in the class

b) who study both subjects

c) who study at least one of the subjects

d) who only study Chemistry.

Solution :

a) Number of students in the class 

= 3 + 5 + 17 + 4

= 29

b) Number of students who study both subjects = 17

c) Number of students who study at least one of the subjects

= 5 + 17 + 4

= 26

d) Number of students who study Chemistry = 5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.