VELOCITY AND ACCELERATION

A car describes a distance x metres in time t seconds along a straight road. If the velocity v is constant, then 

v = ˣ⁄t meter per sec

That is, the slope (gradient) of the distance/time graph shown in the figure below is constant.

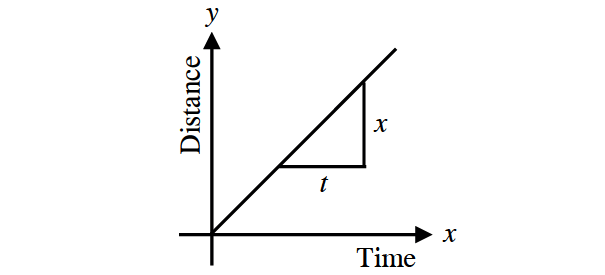
If, however, the velocity of the car is not constant then the distance/time graph will not be a straight line. It may be as shown in the figure below.

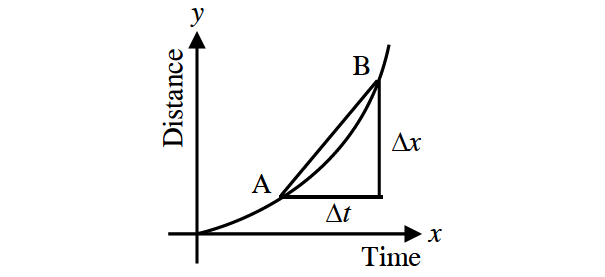
The average velocity over a small time Δt and distance Δx is given by the gradient of the chord AB. That is, the average velocity over time Δt is

As Δt → 0, the chord AB becomes a tangent, such that at point A the velocity is given by v = ᵈˣ⁄dt. Hence the velocity of the car at any instant is given by gradient of the distance/time graph. If an expression for the distance x is known in terms of time, then the velocity is obtained by differentiating the expression.

The acceleration a of the car is defined as the rate of change of velocity. A velocity/time graph is shown in the figure below.

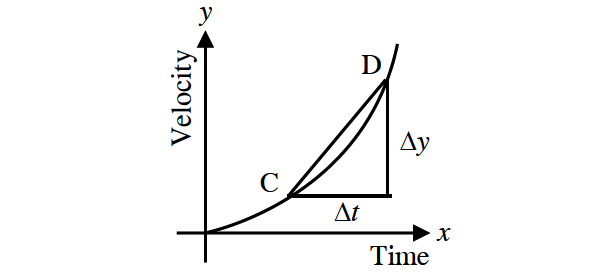
If Δv is the change in v and Δt is the corresponding change in time, then

As Δt → 0 the chord CD becomes a tangent such that at the point C, the acceleration is given by a = ᵈⱽ⁄dt.

Hence the acceleration of the car at any instant is given by the gradient of the velocity/time graph. If an expression for velocity is known in terms of time t, then the acceleration is obtained by differentiating the expression.

Acceleration a = ᵈⱽ⁄dt, where v = ᵈˣ⁄dt

Hence

The acceleration is given by the second differential coefficient of distance x with respect to time t. The above discussion can be summarised as follows. If a body moves a distance x meters in time t seconds then

(i) distance x = f(t).

(ii) velocity v = f'(t) or ᵈˣ⁄dt, which is the gradient of the distance/time graph.

Note :

(i) Initial velocity means velocity at t = 0.

(ii) Initial acceleration means acceleration at t = 0.

(iii) If the motion is upward, at the maximum height, the velocity is zero.

(iv) If the motion is horizontal, v = 0 when the particle comes to rest.

Solved Problems

Problem 1 :

The distance x metres described by a car in time t seconds is given by :

x = 3t³ - 2t² + 4t  - 1

Determine the velocity and acceleration when (i) t = 0 and (ii) t = 1.5 sec.

Solution :

x = 3t³ - 2t² + 4t  - 1

Velocity :

v = ᵈˣ⁄dt

v = 3(3t²) - 2(2t) + 4(1) - 0

v = 9t² - 4t + 4

Acceleration :

a = ᵈⱽ⁄dt

a = 9(2t) - 4(1) + 0

a = 18t - 4

When t = 0,

When t = 1.5 sec.,

Problem 2 :

Supplies are dropped from an helicopter and distance fallen in time t seconds is given by x

x = (½)gt²

where g = 9.8 m/sec². Determine the velocity and acceleration of the supplies after it has fallen for 2 seconds.

Solution :

Distance :

x = (½)gt²

x = (½)(9.8)t²

x = 4.9t²

Velocity :

v = ᵈˣ⁄dt

v = 4.9(2t)

v = 9.8t

Acceleration :

a = ᵈⱽ⁄dt

a = 9.8(1)

a = 9.8

When t = 2 seconds,

Problem 3 :

The angular displacement θ radians of a fly wheel varies with time t seconds and follows the equation

θ = 9t² - 2t³

Determine

(i) the angular velocity and acceleration of the fly wheel when time t = 1 second and

(ii) the time when the angular acceleration is zero.

Solution :

Part (i) :

Angular displacement :

θ = 9t² - 2t³

Angular velocity :

ω = ᵈ^θ⁄dt

ω = 9(2t) - 2(3t²)

ω = 18t - 6t²

Angular acceleration :

α = ᵈ^ω⁄dt

α = 18(1) - 6(2t)

α = 18 - 12t

When t = 1 second,

Part (ii) :

When angular acceleration is zero,

α = 0

18 - 12t = 0

-12t = -18

t = 1.5 seconds

Problem 4 :

A boy, who is standing on a pole of height 14.7 m throws a stone vertically upwards. It moves in a vertical line slightly away from the pole and falls on the ground. Its equation of motion in meters and seconds is

x = 9.8t - 4.9t²

(i) Find the time taken for upward and downward motions.(ii) Also find the maximum height reached by the stone from the ground.

Solution :

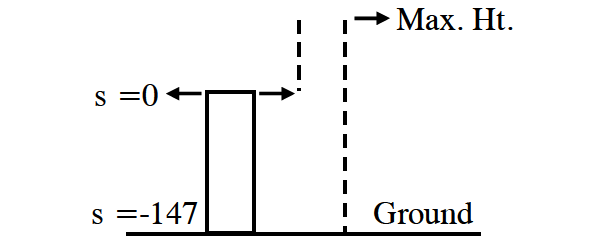
Part (i) :

x = 9.8t - 4.9t²

Velocity :

v = ᵈˣ⁄dt

v = 9.8(1) - 4.9(2t)

v = 9.8 - 9.8t

At the maximum height v = 0.

9.8 - 9.8t = 0

-9.8t = -9.8

t = 1 second

So, the time taken for upward motion is 1 second. For each position x, there corresponds a time t.

The ground position is x = -14.7, since the top of the pole is taken as x = 0.

To get the total time, substitute x = -14.7 into the given equation.

-14.7 = 9.8t - 4.9t²

 4.9t² - 9.8t - 14.7 = 0

Multiply both sides by 10.

 49t² - 98t - 147 = 0

Divide both sides by 49.

t² - 2t - 3 = 0

Factor and solve for t.

t² - 3t + t - 3 = 0

t(t - 3) + 1(t - 3) = 0

(t - 3)(t + 1) = 0

t - 3 = 0  or  t + 1 = 0

t = 3  or  t = -1

Time can never be a negative value. So, t = 3.

Already we know that the time taken for upward motion is t = 1 second.

Therefore, the time taken for downward motion is

= 3 - 1

= 2 seconds

Part (ii) :

When t = 1,

x = 9.8(1) - 4.9(1)²

x = 9.8 - 4.9

x = 9.8

The maximum height reached by the stone :

= 14.7 + 4.9

= 19.6 meters

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.