VELOCITY AND ACCELERATION PROBLEMS FOR AP CALCULUS

Problem 1 :

For 0 ≤ t ≤ 12, a particle moves along the x-axis. The velocity of the particle at time t is given by

v(t)  =  cos (πt/6).

The particle is at position x  =  -2 at time t  =  0.

(a)  For 0 ≤ t ≤ 12 when is the particle moving to the left ?

(b) Write, but do not evaluate, an integral expression that gives the total distance traveled by the particle from time t = 0 to time t = 6.

(c) Find the acceleration of the particle at time t. Is the speed of the particle increasing, decreasing, or neither at time t = 4 ? Explain your reasoning.

(d) Find the position of the particle at time t = 4

Solution :

(a)  When the velocity is negative, it shows that the the particle is moving left side.

v(t)  =  cos (πt/6)

When v(t)  =  0

cos (πt/6)  =  0

πt/6  =  cos^-1(0)

πt/6  =  π/2, 3π/2

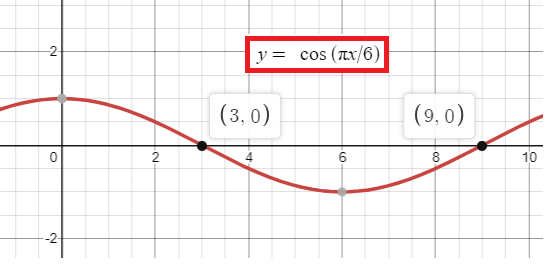
v(t) < 0 when 3 < t < 9

(b) ) integral 0 to 6 v(t) dt

(c)  v(t)  =  cos (πt/6)

a(t)  =  -sin(πt/6) ⋅ (π/6)

a(t)  =  -(π/6) sin(πt/6)

at t  =  4

a(4)  =  -(π/6) sin(4π/6)

a(4)  =  -(π/6) √3/2

a(4)  =  -√3π/12 < 0

v(t)  =  cos (πt/6)

at t  =  4

v(t)  =  cos (4π/6)

v(t)  =  cos (2π/3)

v(t)  =  -1/2 < 0

Since velocity and acceleration have same signs, the speed is increasing.

(d) Find the position of the particle at time t = 4

Given that :

v(t)  =  cos (πt/6)

The distance at t = 0, x  =  -2

x(t)  =  -2 + (Integral t = a to t  = b cos (πt/6))

x(4)  =  -2 + (Integral t = 0 to t  = 4 cos (πt/6))

x(4)  =  -2 + [sin(πt/6)/(π/6)] t = 0 to t = 4

x(4)  =  -2 + (6/π) [sin(πt/6)] t = 0 to t = 4

x(4)  =  -2 + (6/π) [sin 0 - sin (2π/3)]

x(4)  =  -2 + (6/π) (- √3/2)

x(4)  =  -2 -(3√3/π) 

Problem 2 :

For t ≥ 0, a particle moves along the x axis. The velocity of the particle at time t is given by

v(t)  =  1+2sin(t²/2)

The particle is at position x  =  2 at time t  =  4.

(a) At time t  =  4, is the particle speeding up or slowing down.

(b)  Find all times t in the interval 0 < t < 3, when the particle changes its direction. Justify your answer.

(c)  Find the position of the particle at time t  =  0.

Solution :

(a)  v(t)  =  1+2sin(t²/2) (Given)

at t  =  4

v(4)  =  1+2sin(4²/2)

v(4)  =  1+2sin8

=  1 + 2(0.9893)

=  1+1.9786

v(4)  =  2.9786

v(t)  =  1+2sin(t²/2)

a(t)  =  0+2cos(t²/2)(2t/2)

a(t)  =  2tcos(t²/2)

a(4)  =  8cos8

=  8(-0.1455)

a(4)  =  -1.164

Both velocity and acceleration having same sings, so the particle is speeding up.

(b)  v(t)  =  0

v(t)  =  1+2sin(t²/2)

using graphing calculator, finding x-intercepts we get

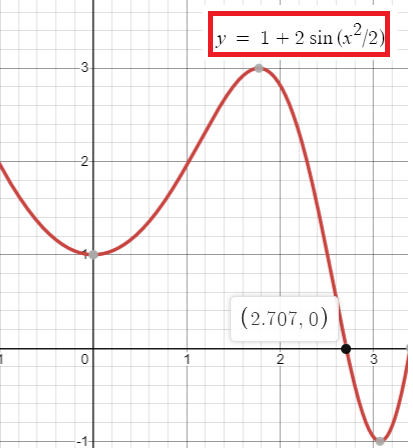
v(t) changes its direction from positive to negative at

t  =  2.707.

(c)  Find the position of the particle at time t  =  0.

x(0)  =  ?

x(t)  =  2 + integral 4 to 0 v(t)

x(4)  =  2 + integral 4 to 0 (1+2sin(t²/2)) dt

Let u  =  t²/2

du  =  (2t/2) dt

du  =  t dt

t  =  √(2u)

dt  =  du/√(2u)

x(4)  =  2 + integral 8 to 0 (1+2sinu) du/√(2u)

x(4)  =  -3.815

Problem 3 :

The position of the particle is given as 

x(t) = cos 3t - sin 4t

Find the acceleration at t = 0.

(A) -9    (B) 0      (C) 1      (D) 2     (E) 16

Solution :

Given that,

x(t) = cos 3t - sin 4t

Finding velocity :

x'(t) = -sin 3t ⋅ (3) - cos (4t) ⋅ 4

= -3 sin 3t - 4 cos (4t)

Finding acceleration :

x'(t) = -3 sin 3t - 4 cos (4t)

x''(t)  = -3 cos 3t ⋅ (3) + 4 sin (4t) ⋅ 4

x''(t) = -9 cos 3t + 16 sin (4t)

Acceleration at t = 0,

x''(0) = -9 cos 3(0) + 16 sin 4(0)

= -9 cos 0 + 16 sin 0

= -9(1) + 16(0)

= -9

Problem 4 :

s(t) = t² - 4t - 96

A particle moves along a horizontal line. Its position function is s(t) for t ≥ 0. For each problem, find the intervals of time when the particle is slowing down and speeding up.

Solution :

s(t) = − t² + t + 72

Finding velocity :

v(t) = −2t + 1

v(t) = 0

−2t + 1 = 0

2t = 1

t = 1/2

Finding acceleration :

a(t) = V'(t) = -2(1) + 0

= -2

There is no values for t.

Decomposing into intervals :

(0, 1/2) and (1/2, ∞)

In the interval (0, 1/2),

0.4 (-2) = -0.8 < 0 (slowing down)

In the interval (1/2, ∞),

-0.2(-2) = 0.4 > 0 (speeding up)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.